Textbook Question
Use the graphs of f and g to solve Exercises 83–90.
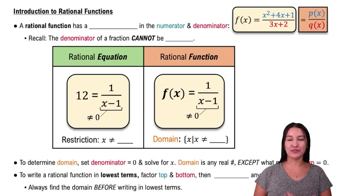
Find the domain of ƒ/g.
708
views
1
rank
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:2m
5:2mMaster Relations and Functions with a bite sized video explanation from Patrick
Start learning