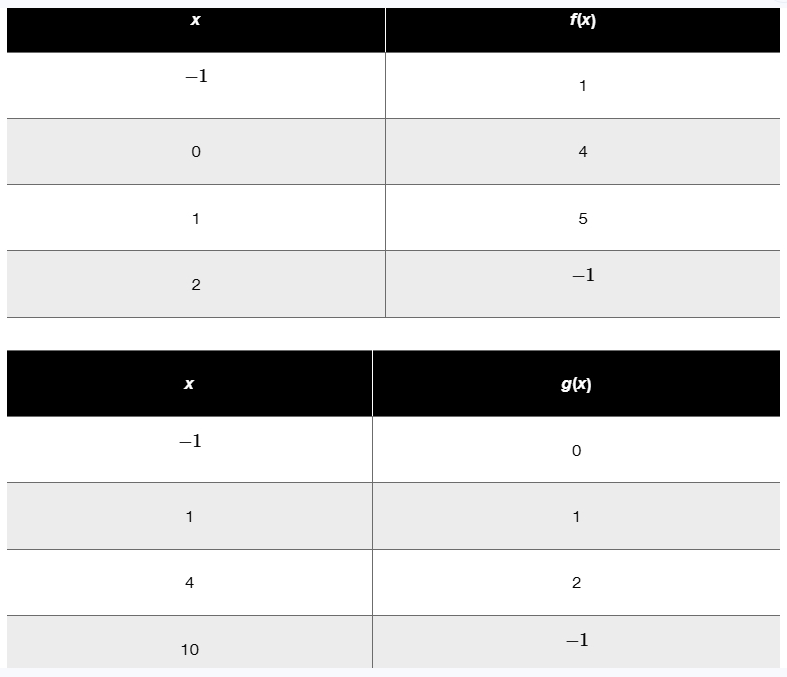
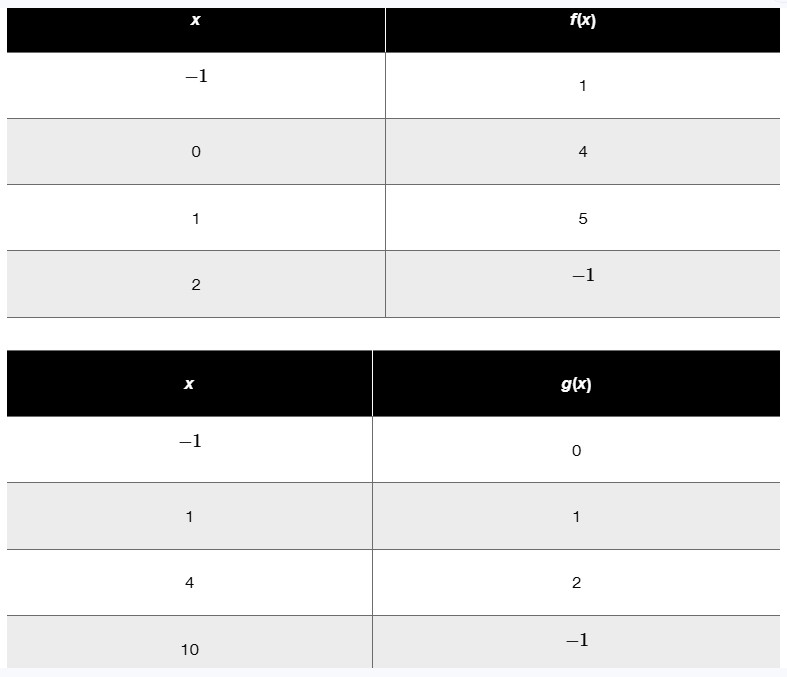
In Exercises 53–58, f and g are defined by the following tables. Use the tables to evaluate each composite function. f(g(1))

In Exercises 53–58, f and g are defined by the following tables. Use the tables to evaluate each composite function. (go f) (-1)

Let f(x) = 2x - 5 g(x) = 4x - 1 h(x) = x² + x + 2. Evaluate the indicated function without finding an equation for the function. (fog) (0)

Let f(x) = 2x - 5 g(x) = 4x - 1 h(x) = x² + x + 2. Evaluate the indicated function without finding an equation for the function. ƒ^-1 (1)

Let f(x) = 2x - 5 g(x) = 4x - 1 h(x) = x² + x + 2. Evaluate the indicated function without finding an equation for the function. f(g[h (1)])

Determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement.

If $f\left(x\right)=3x$ and $g\left(x\right)=x+5$, find ${(f\circ g)}^{-1}\left(x\right)$ and $(g^{-1}\circ f^{-1})\left(x\right)$.

Solve by completing the square: 2x² – 5x + 1 = 0.

Solve: 5x^3/4- 15 = 0.

Solve and graph the solution set on a number line: 3|2x-1| ≥ 21

Exercises 103–105 will help you prepare for the material covered in the next section. Use a rectangular coordinate system to graph the circle with center (1, -1) and radius 1.

Exercises 103–105 will help you prepare for the material covered in the next section. Solve by completing the square: y² – 6y — 4 = 0.

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (2, 3) and (14, 8)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (4, -1) and (-6, 3)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, 0) and (3,-4)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (-2, -6) and (3, −4)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (3.5, 8.2) and (-0.5, 6.2)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, −√3) and (√5, 0)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, -√2) and (√7,0)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (3√3, √5) and (−√3, 4√5)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (7/3, 1/5) and (1/3, 6/5)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (-1/4, -1/7) and (3/4, 6/7)

Find the midpoint of each line segment with the given endpoints. (6, 8) and (2, 4)

Find the midpoint of each line segment with the given endpoints. (-2, -8) and (−6, −2)

Find the midpoint of each line segment with the given endpoints. (-3, -4) and (6, −8)

Find the midpoint of each line segment with the given endpoints. (-7/2, 3/2) and (-5/2, -11/2)

Find the midpoint of each line segment with the given endpoints. (8, 3√5) and (−6, 7√5)

Find the midpoint of each line segment with the given endpoints. (7√3, −6) and (3√3, −2)

Write the standard form of the equation of the circle with the given center and radius. Center (0, 0), r = 7

Write the standard form of the equation of the circle with the given center and radius. Center (3, 2), r = 5

Write the standard form of the equation of the circle with the given center and radius. Center (-1, 4), r = 2