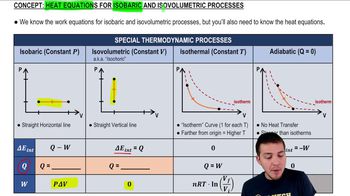
In Problems and you are given the equation(s) used to solve a problem. For each of these, you are to draw a pV diagram.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 7:21m
7:21mMaster Ideal Gases and the Ideal Gas Law with a bite sized video explanation from Patrick
Start learning