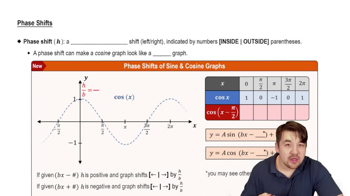
Fill in the blank(s) to correctly complete each sentence.
The graph of y = 3 + 5 cos (x + π/5) is obtained by shifting the graph of y = cos x horizontally ________ unit(s) to the __________, (right/left) stretching it vertically by a factor of ________, and then shifting it vertically ________ unit(s) __________. (up/down)