Suppose the interval [1, 3] is partitioned into n = 4 subintervals. What is the subinterval length ∆𝓍? List the grid points x₀ , x₁ , x₂ , x₃ and x₄. Which points are used for the left, right, and midpoint Riemann sums?

Does a right Riemann sum underestimate or overestimate the area of the region under the graph of a function that is positive and decreasing on an interval [a,b]? Explain.

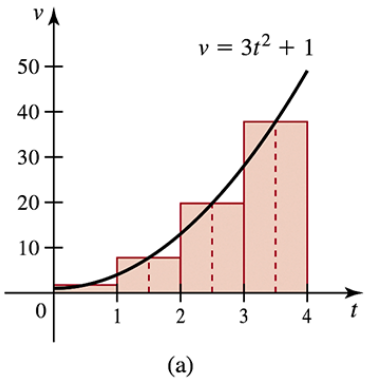
Approximating displacement The velocity in ft/s of an object moving along a line is given by v = 3t² + 1 on the interval 0 ≤ t ≤ 4, where t is measured in seconds.

(a) Divide the interval [0,4] into n = 4 subintervals, [0,1] , [1.2] , [2,3] , and [3,4]. On each subinterval, assume the object moves at a constant velocity equal to v evaluated at the midpoint of the subinterval, and use these approximations to estimate the displacement of the object on [0, 4] (see part (a) of the figure)

{Use of Tech} Riemann sums for larger values of n Complete the following steps for the given function f and interval.

ƒ(𝓍) = 3 √x on [0,4] ; n = 40

(b) Based on the approximations found in part (a), estimate the area of the region bounded by the graph of f and the x-axis on the interval.

{Use of Tech} Riemann sums for larger values of n Complete the following steps for the given function f and interval.

ƒ(𝓍) = x² ― 1 on [2,5] ; n = 75

(b) Based on the approximations found in part (a), estimate the area of the region bounded by the graph of f and the x-axis on the interval.

Approximating displacement The velocity of an object is given by the following functions on a specified interval. Approximate the displacement of the object on this interval by subdividing the interval into n subintervals. Use the left endpoint of each subinterval to compute the height of the rectangles.

v = 2t + 1(m/s), for 0 ≤ t ≤ 8 ; n = 2

Approximating displacement The velocity of an object is given by the following functions on a specified interval. Approximate the displacement of the object on this interval by subdividing the interval into n subintervals. Use the left endpoint of each subinterval to compute the height of the rectangles.

v = [1 / (2t + 1)] (m/s), for 0 ≤ t ≤ 8 ; n = 4

Approximating displacement The velocity of an object is given by the following functions on a specified interval. Approximate the displacement of the object on this interval by subdividing the interval into n subintervals. Use the left endpoint of each subinterval to compute the height of the rectangles.

{Use of Tech} v = 4 √(t +1) (mi/hr) . for 0 ≤ t ≤ 15 ; n = 5     

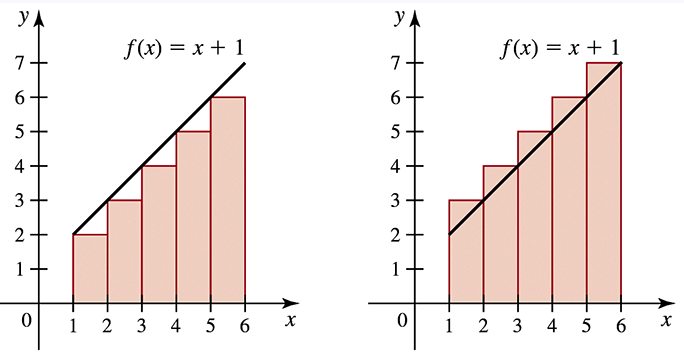
Left and right Riemann sums Use the figures to calculate the left and right Riemann sums for f on the given interval and for the given value of n.

ƒ(𝓍) = x + 1 on [1,6] ; n = 5

Left and right Riemann sums Complete the following steps for the given function, interval, and value of n.​

f(x) = x + 1 on [0,4]; n = 4

(d) Calculate the left and right Riemann sums.                                                                                                                                                

Left and right Riemann sums Complete the following steps for the given function, interval, and value of n.​

{Use of Tech} ƒ(𝓍) = cos 𝓍 on [0. π/2]; n = 4

(d) Calculate the left and right Riemann sums.

Left and right Riemann sums Complete the following steps for the given function, interval, and value of n.

ƒ(𝓍) = x² ─ 1 on [2,4]; n = 4

(d) Calculate the left and right Riemann sums. 

Left and right Riemann sums Complete the following steps for the given function, interval, and value of n.

{Use of Tech} ƒ(𝓍) = e ˣ/₂ on [1,4]; n = 6

(d) Calculate the left and right Riemann sums. 

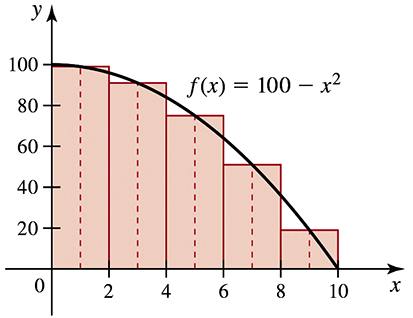
A midpoint Riemann sum Approximate the area of the region bounded by the graph of ƒ(𝓍) = 100 ― x² and the x-axis on [0, 10] with n = 5 subintervals. Use the midpoint of each subinterval to determine the height of each rectangle (see figure).

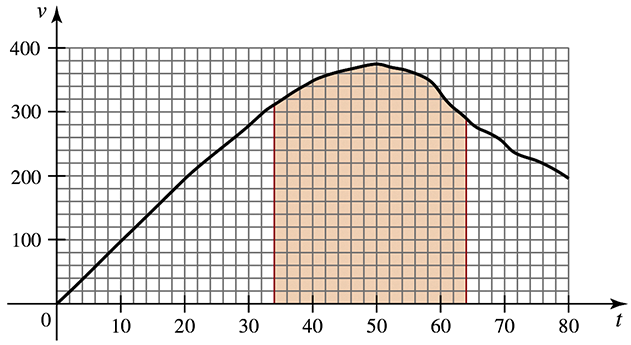
Free fall On October 14, 2012, Felix Baumgartner stepped off a balloon capsule at an altitude of almost 39 km above Earth’s surface and began his free fall. His velocity in m/s during the fall is given in the figure. It is claimed that Felix reached the speed of sound 34 seconds into his fall and that he continued to fall at supersonic speed for 30 seconds. (Source: http://www.redbullstratos.com)

(a) Divide the interval [34, 64] into n = 5 subintervals with the gridpoints x₀ = 34 , x₁ = 40 , x₂ = 46 , x₃ = 52 , x₄ = 58 , and x₅ = 64. Use left and right Riemann sums to estimate how far Felix fell while traveling at supersonic speed.

Midpoint Riemann sums Complete the following steps for the given function, interval, and value of n.​

ƒ(𝓍) = 2x + 1 on [0,4] ; n = 4

d) Calculate the midpoint Riemann sum.

Midpoint Riemann sums Complete the following steps for the given function, interval, and value of n.

{Use of Tech} ƒ(𝓍) = √x on [1,3] ; n = 4

(d) Calculate the midpoint Riemann sum.

Midpoint Riemann sums Complete the following steps for the given function, interval, and value of n.​

ƒ(𝓍) = 1/x on [1,6] ; n = 5

(d) Calculate the midpoint Riemann sum.

Sigma notation Express the following sums using sigma notation. (Answers are not unique.)

(a) 1 + 2 + 3 + 4 + 5

Sigma notation Express the following sums using sigma notation. (Answers are not unique.)

(b) 4 + 5 + 6 + 7 + 8 + 9

Sigma notation Express the following sums using sigma notation. (Answers are not unique.)

(c) 1² + 2² + 3² + 4²

Sigma notation Express the following sums using sigma notation. (Answers are not unique.)

(d) 1 + 1/2 + 1/3 + 1/4

Sigma notation Evaluate the following expressions.

(a)    10                                                                                                                                                                               

       ∑ κ                                                                                                                                                                          

       κ=1                         

Sigma notation Evaluate the following expressions.                                                                                                                                          

(b)    10                                                                                                                                                                               

       ∑  (2κ + 1)                                                                                                                                                                          

       κ=1                         

Sigma notation Evaluate the following expressions.                                                                                                                                          

(c)     4                                                                                                                                                                               

       ∑ κ²                                                                                                                                                                          

       κ=1                         

Sigma notation Evaluate the following expressions.

(d)     5                                                                                                                                                                              

       ∑ (1 + n²)                                                                                                                                                                          

       n=1                         

Sigma notation Evaluate the following expressions.                                                                                                                                          

(e)     3                                                                                                                                                                               

       ∑  (2m + 2) / 3                                                                                                                                                                          

      m =1                         

Sigma notation Evaluate the following expressions.                                                                                                                                          

  (f)      3                                                                                                                                                                               

       ∑ (3j ― 4)                                                                                                                                                                          

      j =1                         

Displacement from a table of velocities The velocities (in mi/hr) of an automobile moving along a straight highway over a two-hour period are given in the following table.

(b) Find the midpoint Riemann sum approximation to the displacement on [0,2] with n = 2 and .n = 4 . ​

Displacement from velocity The following functions describe the velocity of a car (in mi/hr) moving along a straight highway for a 3-hr interval. In each case, find the function that gives the displacement of the car over the interval [0,t], where 0 ≤ t ≤ 3.

v(t) = { 30 if 0 ≤ t ≤ 2

50 if 2 < t < 2.5

44 if 2.5 < t ≤ 3