Back
BackProblem 5.R.96c
Velocity to displacement An object travels on the 𝓍-axis with a velocity given by v(t) = 2t + 5, for 0 ≤ t ≤ 4.
(c) True or false: The object would travel as far as in part (a) if it traveled at its average velocity (a constant), for 0 ≤ t ≤ 4. .
Problem 5.R.97
Find the average value of ƒ(𝓍) = e²ˣ on [0, ln 2] .
Problem 5.R.102a
Function defined by an integral Let H (𝓍) = ∫₀ˣ √(4 ― t²) dt, for ― 2 ≤ 𝓍 ≤ 2.
(a) Evaluate H (0) .
Problem 5.R.102c
Function defined by an integral Let H (𝓍) = ∫₀ˣ √(4 ― t²) dt, for ― 2 ≤ 𝓍 ≤ 2.
(c) Evaluate H '(2) .
Problem 5.R.102e
Function defined by an integral Let H (𝓍) = ∫₀ˣ √(4 ― t²) dt, for ― 2 ≤ 𝓍 ≤ 2.
(e) Find the value of s such that H (𝓍) = sH(―𝓍)
Problem 5.R.107
Limits with integrals Evaluate the following limits.
lim ∫₂ˣ eᵗ² dt
𝓍→2 ---------------
𝓍 ― 2
Problem 5.R.113c
Function defined by an integral Let ƒ(𝓍) = ∫₀ˣ (t ― 1)¹⁵ (t―2)⁹ dt .
(c) For what values of 𝓍 does ƒ have local minima? Local maxima?
Problem 5.R.104
Change of variables Use the change of variables u³ = 𝓍² ― 1 to evaluate the integral ∫₁³ 𝓍∛(𝓍²―1) d𝓍 .
Problem 5.R.99b
(b) Find the average value of ƒ shown in the figure on the interval [2,6] and then find the point(s) c in (2, 6) guaranteed to exist by the Mean Value Theorem for Integrals.
Problem 5.R.109
Geometry of integrals Without evaluating the integrals, explain why the following statement is true for positive integers n:
∫₀¹ 𝓍ⁿd𝓍 + ∫₀¹ ⁿ√(𝓍d𝓍) = 1
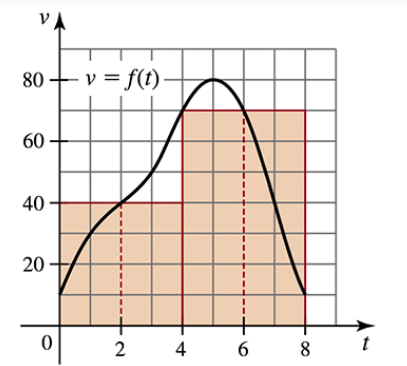
Problem 5.1.71a
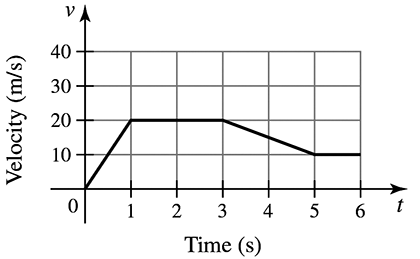
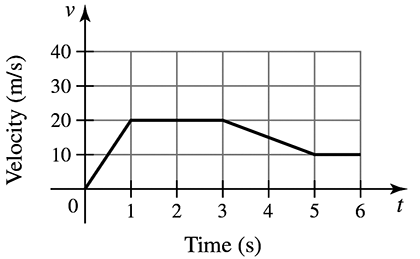
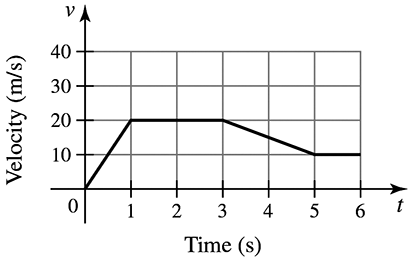
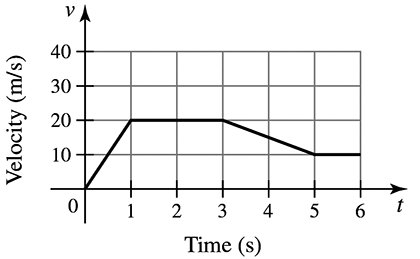
Displacement from a velocity graph Consider the velocity function for an object moving along a line (see figure).
(a) Describe the motion of the object over the interval [0,6].
Problem 5.1.71b
Displacement from a velocity graph Consider the velocity function for an object moving along a line (see figure).
(b) Use geometry to find the displacement of the object between t = 0 and t = 2.
Problem 5.1.71c
Displacement from a velocity graph Consider the velocity function for an object moving along a line (see figure).
(c) Use geometry to find the displacement of the object between t = 2 and t = 5.
Problem 5.1.71d
Displacement from a velocity graph Consider the velocity function for an object moving along a line (see figure).
(d) Assuming the velocity remains 10 m/s, for t ≥ 5, find the function that gives the displacement between t = 0 and any time t ≥ 5.
Problem 5.1.73a
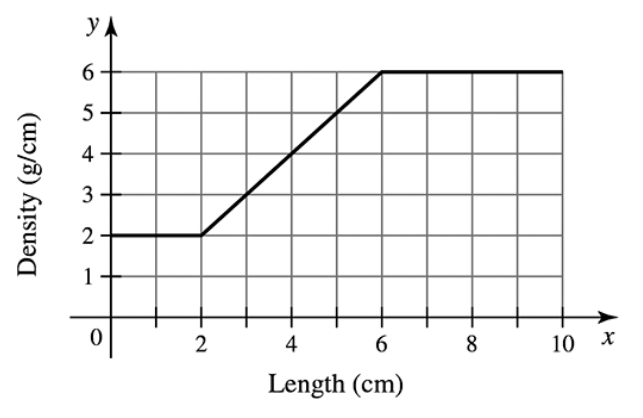
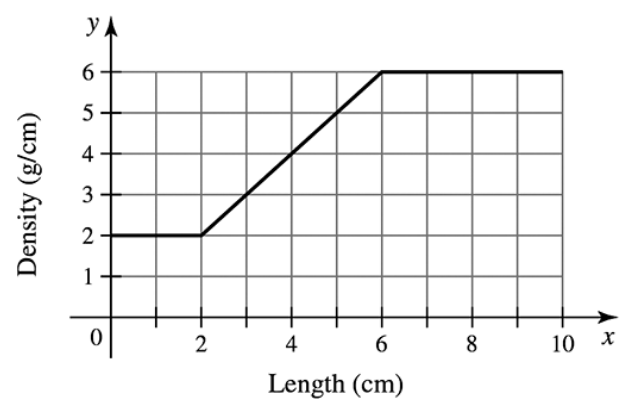
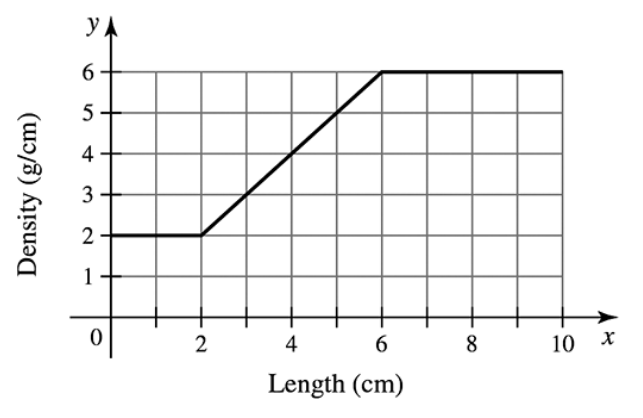
Mass from density A thin 10-cm rod is made of an alloy whose density varies along its length according to the function shown in the figure. Assume density is measured in units of g/cm. In Chapter 6, we show that the mass of the rod is the area under the density curve.
(a) Find the mass of the left half of the rod (0 ≤ x ≤ 5) .
Problem 5.1.73b
Mass from density A thin 10-cm rod is made of an alloy whose density varies along its length according to the function shown in the figure. Assume density is measured in units of g/cm. In Chapter 6, we show that the mass of the rod is the area under the density curve.
(b) Find the mass of the right half of the rod (5 ≤ x ≤ 10) .
Problem 5.1.73c
Mass from density A thin 10-cm rod is made of an alloy whose density varies along its length according to the function shown in the figure. Assume density is measured in units of g/cm. In Chapter 6, we show that the mass of the rod is the area under the density curve.
(c) Find the mass of the entire rod (0 ≤ x ≤ 10) .
Problem 5.1.1
Suppose an object moves along a line at 15 m/s, for 0 ≤ t < 2 and at 25 m/s, for 2 ≤ t ≤ 5, where t is measured in seconds. Sketch the graph of the velocity function and find the displacement of the object for 0 ≤ t ≤ 5.
Problem 5.1.3a
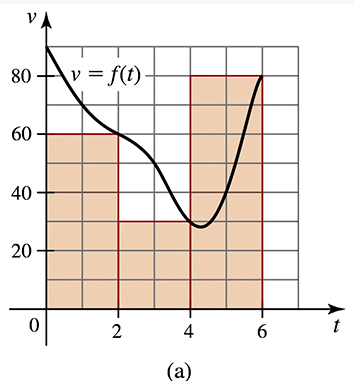
The velocity in ft/s of an object moving along a line is given by v = ƒ(t) on the interval 0 ≤ t ≤ 8 (see figure), where t is measured in seconds.
a) Divide the interval [0,8] into n = 2 subintervals, [0,4] and [4,8]. On each subinterval, assume the object moves at a constant velocity equal to the value of v evaluated at the midpoint of the subinterval, and use these approximations to estimate the displacement of the object on [0,8] (see part (a) of the figure)
Problem 5.1.5a
The velocity in ft/s of an object moving along a line is given by v = ƒ(t) on the interval 0 ≤ t ≤ 6 (see figure), where t is measured in seconds.
(a) Divide the interval [0,6] into n = 3 subintervals, [0,2] , [2,4] and [4,6]. On each subinterval, assume the object moves at a constant velocity equal to the value of v evaluated at the right endpoint of the subinterval, and use these approximations to estimate the displacement of the object on [0,6] (see part (a) of the figure)
Problem 5.1.67
Identifying Riemann sums Fill in the blanks with an interval and a value of n.
4
∑ ƒ (1.5 + k) • 1 is a midpoint Riemann sum for f on the interval [ ___ , ___ ]
k = 1
with n = ________ .
Problem 5.1.65
Identifying Riemann sums Fill in the blanks with an interval and a value of n.
4
∑ ƒ (1 + k) • 1 is a right Riemann sum for f on the interval [ ___ , ___ ] with
k = 1
n = ________ .
Problem 5.1.63
{Use of Tech} Sigma notation for Riemann sums Use sigma notation to write the following Riemann sums. Then evaluate each Riemann sum using Theorem 5.1 or a calculator.
The midpoint Riemann sum for f(x) = x³ on [3,11] with n = 32.
Problem 5.1.61
{Use of Tech} Sigma notation for Riemann sums Use sigma notation to write the following Riemann sums. Then evaluate each Riemann sum using Theorem 5.1 or a calculator.
The right Riemann sum for ƒ(𝓍)) = x + 1 on [0, 4] with n = 50.
Problem 5.1.59c
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(c) For an increasing or decreasing nonconstant function on an interval [a,b] and a given value of n, the value of the midpoint Riemann sum always lies between the values of the left and right Riemann sums.
Problem 5.1.59b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(b) A left Riemann sum always overestimates the area of a region bounded by a positive increasing function and the x-axis on an interval [a,b].
Problem 5.1.59a
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(a) Consider the linear function ƒ(𝓍) = 2x + 5 and the region bounded by its graph and the x-axis on the interval [3,6]. Suppose the area of this region is approximated using midpoint Riemann sums. Then the approximations give the exact area of the region for any number of subintervals.
Problem 5.1.69a
Approximating areas Estimate the area of the region bounded by the graph of ƒ(𝓍) = x² + 2 and the x-axis on [0, 2] in the following ways.
(a) Divide [0, 2] into n = 4 subintervals and approximate the area of the region using a left Riemann sum. Illustrate the solution geometrically.
Problem 5.1.69c
Approximating areas Estimate the area of the region bounded by the graph of ƒ(𝓍) = x² + 2 and the x-axis on [0, 2] in the following ways.
(c) Divide [0, 2] into n = 4 subintervals and approximate the area of the region using a right Riemann sum. Illustrate the solution geometrically.
Problem 5.1.9
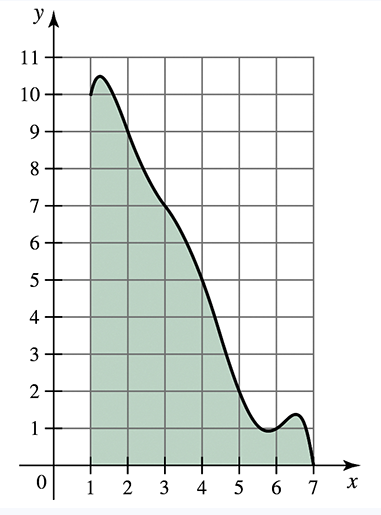
Approximating area from a graph Approximate the area of the region bounded by the graph (see figure) and the 𝓍-axis by dividing the interval [1, 7] into n = 6 subintervals. Use a left and right Riemann sum to obtain two different approximations.

![Graph of a function f(x) with a peak at (4,5) on the interval [2,6], showing axes labeled x and y.](https://static.studychannel.pearsonprd.tech/courses/calculus/thumbnails/644163eb-ecf8-4691-b0f1-f30360c250e2)