Back
Problem 5.R.41
Evaluating integrals Evaluate the following integrals.
β« (9πβΈβ7πβΆ) dπ
Problem 5.R.51
Evaluating integrals Evaluate the following integrals.
β« πΒ² cos πΒ³ dπ
Problem 5.R.53
Evaluating integrals Evaluate the following integrals.
β« (cos 7Ο) /(16 + sinΒ² 7Ο) dΟ
Problem 5.R.54
Evaluating integrals Evaluate the following integrals.
β«(β1 + tan 2t) secΒ² 2t dt
Problem 5.R.60
Evaluating integrals Evaluate the following integrals.
β« sin π΅ sin (cos π΅) dπ΅
Problem 5.R.62
Evaluating integrals Evaluate the following integrals.
β« yΒ² /(yΒ³ + 27) dy
Problem 5.R.64
Evaluating integrals Evaluate the following integrals.
β« yΒ² (3yΒ³ + 1)β΄ dy
Problem 5.R.66
Evaluating integrals Evaluate the following integrals.
β« π sin πΒ² cosβΈ πΒ² dπ
Problem 5.R.75
Evaluating integrals Evaluate the following integrals.
β« dπ/[(tanβ»ΒΉ π) (1 + πΒ²)]
Problem 5.R.78
Evaluating integrals Evaluate the following integrals.
β« πβ· β(πβ΄ + 1dπ)
Problem 5.RE.15a
Symmetry properties Suppose β«ββ΄ Ζ(π) dπ = 10 and β«ββ΄ g(π) dπ = 20. Furthermore, suppose Ζ is an even function and g is an odd function. Evaluate the following integrals.
(a) β«βββ΄ Ζ(π) dπ
Problem 5.RE.15e
Symmetry properties Suppose β«ββ΄ Ζ(π) dπ = 10 and β«ββ΄ g(π) dπ = 20. Furthermore, suppose Ζ is an even function and g is an odd function. Evaluate the following integrals.
(e) β«ββΒ² 3πΖ(π)dπ
Problem 5.RE.15c
Symmetry properties Suppose β«ββ΄ Ζ(π) dπ = 10 and β«ββ΄ g(π) dπ = 20. Furthermore, suppose Ζ is an even function and g is an odd function. Evaluate the following integrals.
(c) β«βββ΄ (4Ζ(π) β 3g(π))dπ
Problem 5.R.1a
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(a) A(π) = β«βΛ£ Ζ(t) dt and Ζ(t) = 2tβ3 , then A is a quadratic function.
Problem 5.R.1b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(b) Given an area function A(π) = β«βΛ£ Ζ(t) dt and an antiderivative F of Ζ, it follows that A'(π) = F(π) .
Problem 5.R.1c
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(c) β«βα΅ Ζ'(π) dπ = Ζ(b) βΖ(a) .
Problem 5.R.1d
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(d) If Ζ is continuous on [a,b] and β«βα΅ |Ζ(π)| dπ = 0 , then Ζ(π) = 0 on [a,b] .
Problem 5.R.25
Use geometry and properties of integrals to evaluate the following definite integrals.β
β«ββ΄ β(8πβπΒ²) dπ . (Hint: Complete the square .)
Problem 5.R.87
Area of regions Compute the area of the region bounded by the graph of Ζ and the π-axis on the given interval. You may find it useful to sketch the region.
Ζ(π)β = 16βπΒ² on [β4, 4]
Problem 5.R.89
Area of regions Compute the area of the region bounded by the graph of Ζ and the π-axis on the given interval. You may find it useful to sketch the region.
Ζ(π)β = 2 sin π/4 on [0, 2Ο]
Problem 5.R.91
Area versus net area Find (i) the net area and (ii) the area of the region bounded by the graph of Ζ and the π-axis on the given interval. You may find it useful to sketch the region.β
Ζ(π) = πβ΄ β πΒ² on [β1, 1]
Problem 5.R.1f
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(f) β«βα΅ (2 Ζ(π) β3g (π)) dπ = 2 β«βα΅ Ζ(π) dπ + 3 β«βα΅ g(π) dπ .
Problem 5.R.1g
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume Ζ and Ζ' are continuous functions for all real numbers.
(g) β« Ζ' (g(π))g' (π) d(π) = Ζ(g(π)) + C .
Problem 5.R.23b
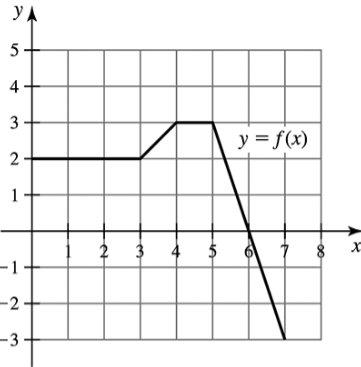
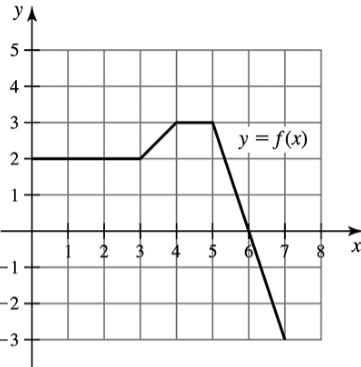
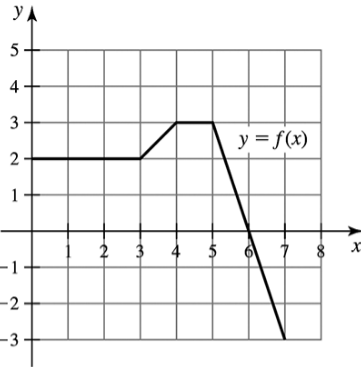
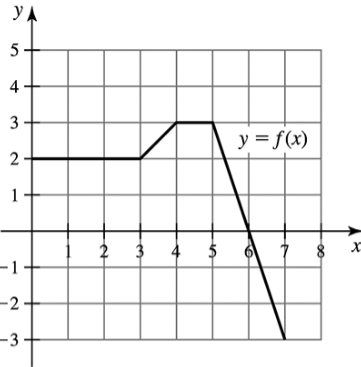
Area by geometry Use geometry to evaluate the following definite integrals, where the graph of Ζ is given in the figure.
(b) β«ββ΄ Ζ(π) dπ
Problem 5.R.23c
Area by geometry Use geometry to evaluate the following definite integrals, where the graph of Ζ is given in the figure.
(c) β«β β· Ζ(π) dπ
Problem 5.R.23d
Area by geometry Use geometry to evaluate the following definite integrals, where the graph of Ζ is given in the figure.
(d) β«ββ· Ζ(π) dπ
Problem 5.R.23a
Area by geometry Use geometry to evaluate the following definite integrals, where the graph of Ζ is given in the figure.
(a) β«ββ΄ Ζ(π) dπ
Problem 5.R.26
Use geometry and properties of integrals to evaluate the following definite integrals.
β«ββ° (2π + β(16βπΒ²)) dπ . (Hint: Write the integral as sum of two integrals.)
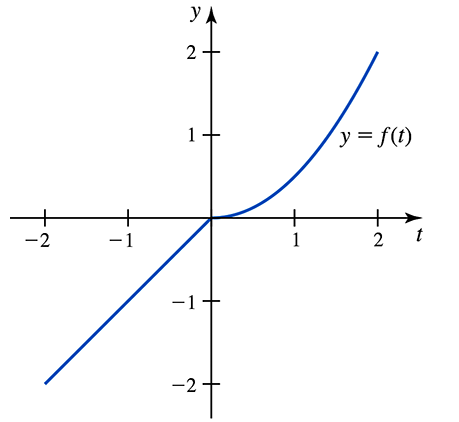
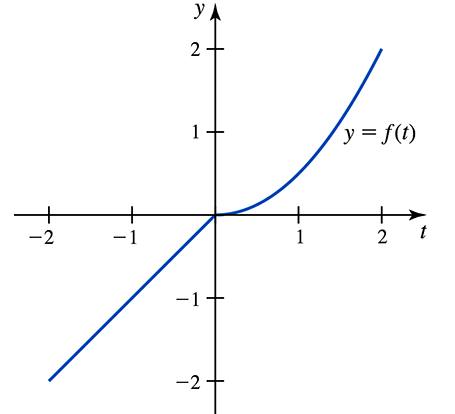
Problem 5.R.105a
Area functions and the Fundamental Theorem Consider the function
Ζ(t) = { t if β2 β€ t < 0
tΒ²/2 if 0 β€ t β€ 2
and its graph shown below. Let F(π) = β«ββΛ£ Ζ(t) dt and G(π) = β«ββΛ£ Ζ(t) dt.
(a) Evaluate F(β2) and F(2).
Problem 5.R.105b
Area functions and the Fundamental Theorem Consider the function
Ζ(t) = { t if β2 β€ t < 0
tΒ²/2 if 0 β€ t β€ 2
and its graph shown below. Let F(π) = β«ββΛ£ Ζ(t) dt and G(π) = β«ββΛ£ Ζ(t) dt.
(b) Use the Fundamental Theorem to find an expression for F '(π) for β2 β€ π < 0.
