Back
BackProblem 6.R.11a
{Use of Tech} Decreasing velocity A projectile is fired upward, and its velocity in m/s is given by v(t) = 200e^−t/10, for t≥0.
a. Graph the velocity function, for t≥0.
Problem 6.R.12a
{Use of Tech} Decreasing velocity A projectile is fired upward, and its velocity (in m/s) is given by v(t) = 200 / √t+1, for t≥0.
a. Graph the velocity function, for t≥0.
Problem 6.R.17
14–25. {Use of Tech} Areas of regions Determine the area of the given region.
The region bounded by y = ln x,y = 1, and x = 1
Problem 6.R.21
14–25. {Use of Tech} Areas of regions Determine the area of the given region.
The region bounded by y = x²,y = 2x²−4x, and y = 0
Problem 6.R.23
14–25. {Use of Tech} Areas of regions Determine the area of the given region.
The region in the first quadrant bounded by y = x/6 and y = 1−|x/2−1|
Problem 6.R.34a
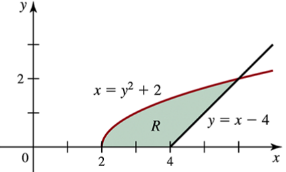
Area and volume The region R is bounded by the curves x = y²+2,y=x−4, and y=0 (see figure).
a. Write a single integral that gives the area of R.
Problem 6.R.7a
An oscillator The acceleration of an object moving along a line is given by a(t) = 2 sin πt/4. The initial velocity and position are v(0)= −8/π and s(0)=0.
a. Find the velocity and position for t≥0.
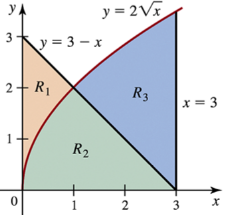
Problem 6.R.27
27–33. Multiple regions The regions R₁,R₂, and R₃ (see figure) are formed by the graphs of y = 2√x,y = 3−x,and x=3.
Find the area of each of the regions R₁,R₂, and R₃.
Problem 6.R.15
14–25. {Use of Tech} Areas of regions Determine the area of the given region.
Problem 6.R.58
58–61. Arc length Find the length of the following curves.
y = 2x+4 on [−2,2] (Use calculus.)
Problem 6.R.66b
Surface area and volume Let f(x) = 1/3 x³ and let R be the region bounded by the graph of f and the x-axis on the interval [0, 2].
b. Find the volume of the solid generated when R is revolved about the y-axis.
Problem 6.R.66c
Surface area and volume Let f(x) = 1/3 x³ and let R be the region bounded by the graph of f and the x-axis on the interval [0, 2].
c. Find the volume of the solid generated when R is revolved about the x-axis.
Problem 6.R.68
Surface area of a cone Find the surface area of a cone (excluding the base) with radius 4 and height 8 using integration and a surface area integral.
Problem 6.RE.1b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
b. Given only the velocity of an object moving on a line, it is possible to find its displacement, but not its position.
Problem 6.RE.1c
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
c. If water flows into a tank at a constant rate (for example, 6 gal/min), the volume of water in the tank increases according to a linear function of time.
Problem 6.R.35
35-38. Area and volume Let R be the region in the first quadrant bounded by the graph of
Find the area of the region R.
Problem 6.R.41
An area function Consider the functions y = x²/a and y = √x/a, where a>0. Find A(a), the area of the region between the curves.
Problem 6.R.73b
Spring work
b. It takes 50 N of force to stretch a spring 0.2 m from its equilibrium position. How much work is needed to stretch it an additional 0.5 m?
Problem 6.R.5
Position, displacement, and distance A projectile is launched vertically from the ground at t=0, and its velocity in flight (in m/s) is given by v(t)=20−10t. Find the position, displacement, and distance traveled after t seconds, for 0≤t≤4.
Problem 6.RE.9a
Fuel consumption A small plane in flight consumes fuel at a rate (in gal/min) given by
R'(t) ={ 4t^{1/3} if 0 ≤ t ≤ 8 (take-off)
2 if t> 0 (cruising)
a. Find a function R that gives the total fuel consumed, for 0≤t≤8.
Problem 6.RE.3d
2–3. Displacement, distance, and position Consider an object moving along a line with the following velocities and initial positions. Assume time t is measured in seconds and velocities have units of m/s.
d. Determine the position function s(t) using the Fundamental Theorem of Calculus (Theorem 6.1). Check your answer by finding the position function using the antiderivative method.
v(t) = 12t²-30t+12, for 0 ≤ t ≤ 3; s(0)=1
Problem 6.R.76
Lifting problem A 4-kg mass is attached to the bottom of a 5-m, 15-kg chain. If the chain hangs from a platform, how much work is required to pull the chain and the mass onto the platform?
Problem 6.RE.72
70–72. Variable density in one dimension Find the mass of the following thin bars.
A bar on the interval 0≤x≤6 with a density ρ(x) = {1 if 0 ≤ x < 2
2 if 2 ≤ x < 4
4 if 4 ≤ x ≤ 6
Problem 6.R.77b
Pumping water A water tank has the shape of a box that is 2 m wide, 4 m long, and 6 m high.
b. If the water in the tank is 2 m deep, how much work is required to pump the water to a level of 1 m above the top of the tank?
Problem 6.R.42a
Two methods The region R in the first quadrant bounded by the parabola y = 4-x² and coordinate axes is revolved about the y-axis to produce a dome-shaped solid. Find the volume of the solid in the following ways:
a. Apply the disk method and integrate with respect to y.
Problem 6.R.42b
Two methods The region R in the first quadrant bounded by the parabola y = 4-x² and coordinate axes is revolved about the y-axis to produce a dome-shaped solid. Find the volume of the solid in the following ways:
b. Apply the shell method and integrate with respect to x.
Problem 6.R.34b
Area and volume The region R is bounded by the curves x = y²+2,y=x−4, and y=0 (see figure).
b. Write a single integral that gives the volume of the solid generated when R is revolved about the x-axis.
Problem 6.RE.68f
Variable gravity At Earth’s surface, the acceleration due to gravity is approximately g=9.8 m/s² (with local variations). However, the acceleration decreases with distance from the surface according to Newton’s law of gravitation. At a distance of y meters from Earth’s surface, the acceleration is given by a(y) = - g / (1+y/R)², where R=6.4×10⁶ m is the radius of Earth.
f. Graph ymax as a function of v0. What is the maximum height when v0=500 m/s,1500 m/s, and 5 km/s?
Problem 6.R.44
43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.
What is the volume of the solid whose base is the region in the first quadrant bounded by y = √x,y = 2-x, and the x-axis, and whose cross sections perpendicular to the base and parallel to the y-axis are semicircles?
Problem 6.R.47
43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.
The region bounded by the curve y = 1+√x, the curve y = 1−√x, and the line x=1 is revolved about the y-axis. Find the volume of the resulting solid by (a) integrating with respect to x and (b) integrating with respect to y. Be sure your answers agree.