Briggs - Calculus: Early Transcendentals 3rd Edition

Ch. 5 - Integration

Back

All textbooks

Briggs 3rd Edition

Ch. 5 - Integration

Problem 5.2.23b

{Use of Tech} Approximating net area The following functions are positive and negative on the given interval.

f(x) = sin 2x on [0,3π/4]

(b) Approximate the net area bounded by the graph of f and the x-axis on the interval using a left, right, and midpoint Riemann sum with n = 4.

Problem 5.2.24b

{Use of Tech} Approximating net area The following functions are positive and negative on the given interval.

f(𝓍) = x³ on [-1,2]

(b) Approximate the net area bounded by the graph of f and the x-axis on the interval using a left, right, and midpoint Riemann sum with n = 4.

Problem 5.2.77b

{Use of Tech} Midpoint Riemann sums with a calculator Consider the following definite integrals.

(b) Evaluate each sum using a calculator with n = 20, 50, and 100. Use these values to estimate the value of the integral.

∫₀⁴ (4𝓍― 𝓍²) d𝓍

Problem 5.2.75b

{Use of Tech} Midpoint Riemann sums with a calculator Consider the following definite integrals.

(b) Evaluate each sum using a calculator with n = 20, 50, and 100. Use these values to estimate the value of the integral.

∫₁⁴ 2√𝓍 d𝓍

Problem 5.2.75a

{Use of Tech} Midpoint Riemann sums with a calculator Consider the following definite integrals.

(a) Write the midpoint Riemann sum in sigma notation for an arbitrary value of n.

∫₁⁴ 2√𝓍 d𝓍

Problem 5.2.73b

{Use of Tech} Approximating definite integrals with a calculator Consider the following definite integrals.

(b) Evaluate each sum using a calculator with n = 20, 50, and 100. Use these values to estimate the value of the integral.

∫₀¹ cos ⁻¹ 𝓍 d𝓍

Problem 5.2.73a

{Use of Tech} Approximating definite integrals with a calculator Consider the following definite integrals.

(a) Write the left and right Riemann sums in sigma notation for an arbitrary value of n.

∫₀¹ cos ⁻¹ 𝓍 d𝓍

Problem 5.2.71b

{Use of Tech} Approximating definite integrals with a calculator Consider the following definite integrals.

(b) Evaluate each sum using a calculator with n = 20, 50, and 100. Use these values to estimate the value of the integral.

∫₀¹ (𝓍² + 1) d𝓍

Problem 5.2.26b

The following functions are positive and negative on the given interval.

ƒ(𝓍) = xe⁻ˣ on [-1,1]

(b) Approximate the net area bounded by the graph of f and the x-axis on the interval using a left, right, and midpoint Riemann sum with n = 4.

Problem 5.2.35

Identifying definite integrals as limits of sums Consider the following limits of Riemann sums for a function ƒ on [a,b]. Identify ƒ and express the limit as a definite integral.

lim ∑ (𝓍ₖ*² + 1) ∆𝓍ₖ on [0,2]

∆ → 0 k=1

Problem 5.2.37

Identifying definite integrals as limits of sums Consider the following limits of Riemann sums for a function ƒ on [a,b]. Identify ƒ and express the limit as a definite integral.

lim ∑ 𝓍*ₖ (ln 𝓍*ₖ) ∆𝓍ₖ on [1,2]

∆ → 0 k=1

Problem 5.2.45

Definite integrals Use geometry (not Riemann sums) to evaluate the following definite integrals. Sketch a graph of the integrand, show the region in question, and interpret your result.

∫₀⁴ ƒ(𝓍) d𝓍, where ƒ(𝓍) = {5 if 𝓍 ≤ 2

3𝓍 ― 1 if 𝓍 > 2

Problem 5.2.69a

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

(a) If ƒ is a constant function on the interval [a,b], then the right and left Riemann sums give the exact value of ∫ₐᵇ ƒ(𝓍) d𝓍, for any positive integer n.

Problem 5.2.69b

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

(b) If ƒ is a linear function on the interval [a,b] , then a midpoint Riemann sums give the exact value of ∫ₐᵇ ƒ(𝓍) d𝓍, for any positive integer n.

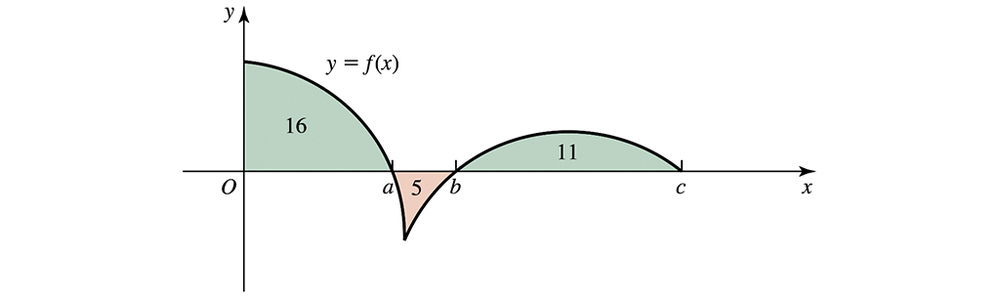
Problem 5.2.65

Definite integrals from graphs The figure shows the areas of regions bounded by the graph of ƒ and the 𝓍-axis. Evaluate the following integrals.

∫ₐ⁰ ƒ(𝓍) d𝓍

Problem 5.2.67

Use geometry and properties of integrals to evaluate

∫₀¹ (2𝓍 + √(1―𝓍²) + 1) d𝓍

Problem 5.2.39

Definite integrals Use geometry (not Riemann sums) to evaluate the following definite integrals. Sketch a graph of the integrand, show the region in question, and interpret your result.

∫₀⁴ (8―2𝓍) d𝓍

Problem 5.2.41

Definite integrals Use geometry (not Riemann sums) to evaluate the following definite integrals. Sketch a graph of the integrand, show the region in question, and interpret your result.

∫₋₁² ( ―|𝓍| ) d𝓍

Problem 5.2.43

Definite integrals Use geometry (not Riemann sums) to evaluate the following definite integrals. Sketch a graph of the integrand, show the region in question, and interpret your result.

∫₀⁴ √(16― 𝓍² ) d𝓍

Problem 5.2.59

Definite integrals from graphs The figure shows the areas of regions bounded by the graph of ƒ and the 𝓍-axis. Evaluate the following integrals.

∫₀ᵃ ƒ(𝓍) d𝓍

Problem 5.2.61

Definite integrals from graphs The figure shows the areas of regions bounded by the graph of ƒ and the 𝓍-axis. Evaluate the following integrals.

∫ₐᶜ ƒ(𝓍) d𝓍

Problem 5.2.63

Definite integrals from graphs The figure shows the areas of regions bounded by the graph of ƒ and the 𝓍-axis. Evaluate the following integrals.

∫₀ᶜ |ƒ(𝓍)| d𝓍

Problem 5.2.29

Area versus net area Graph the following functions. Then use geometry (not Riemann sums) to find the area and the net area of the region described.

The region between the graph of y = 1 - |x| and the x-axis, for -2 ≤ x ≤ 2