Back
Problem 5.3.59
Definite integrals Evaluate the following integrals using the Fundamental Theorem of Calculus
β«βΒ² (zΒ² + 4) / z dz
Problem 5.3.66
Area Find (i) the net area and (ii) the area of the following regions. Graph the function and indicate the region in question.
The region bounded by y = 6 cos π and the π-axis between π = βΟ/2 and π = Ο
Problem 5.3.68
Areas of regions Find the area of the region bounded by the graph of Ζ and the π-axis on the given interval.
Ζ(π) = πΒ³ β 1 on [β1, 2]
Problem 5.3.71
Areas of regions Find the area of the region bounded by the graph of Ζ and the π-axis on the given interval.
Ζ(π) = sin π on [βΟ/4, 3Ο/4]
Problem 5.3.73
Derivatives of integrals Simplify the following expressions.
d/dπ β«βΛ£ (tΒ² + t + 1) dt
Problem 5.3.81
Derivatives of integrals Simplify the following expressions.
d/dz β«ΒΉβ°βα΅’β β dt /(tβ΄ + 1)
Problem 5.3.82
Derivatives of integrals Simplify the following expressions.
d/dy β«ΒΉβ°α΅§Β³ β(πβΆ + 1) dπ
Problem 5.3.84
Derivatives of integrals Simplify the following expressions.
d/dt β«βα΅ dπ/(1 + πΒ²) + β«βΒΉ/α΅ dx/(1 + πΒ²)
Problem 5.3.14a
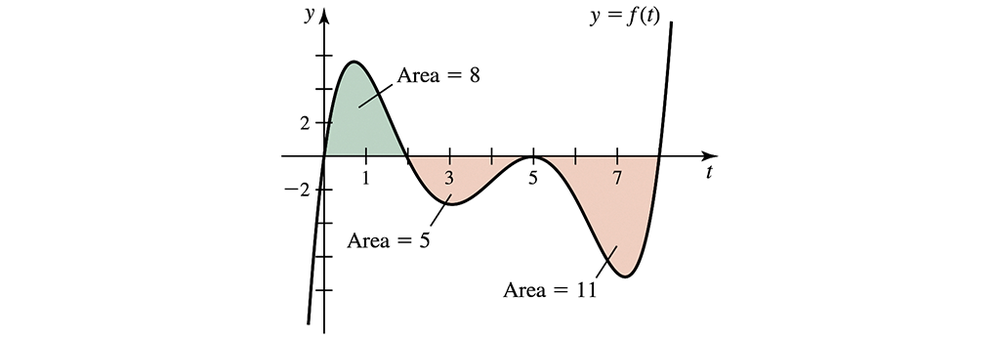
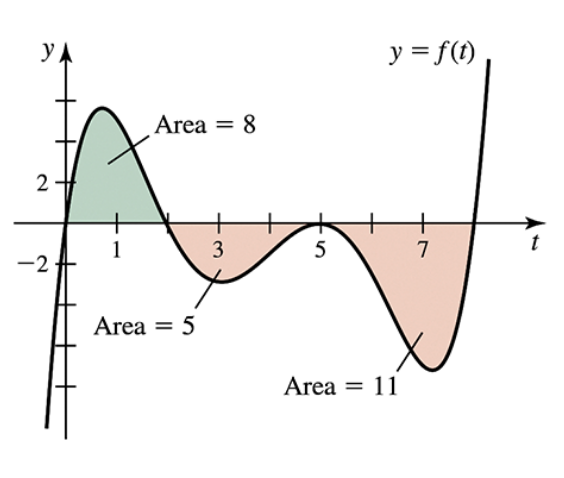
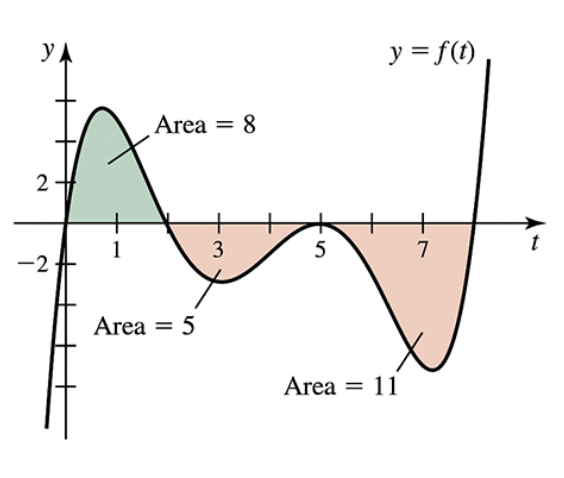
Area functions The graph of Ζ is shown in the figure. Let A(x) = β«βΛ£ Ζ(t) dt and F(x) = β«βΛ£ Ζ(t) dt be two area functions for Ζ. Evaluate the following area functions.
(a) A(2)
Problem 5.3.14d
Area functions The graph of Ζ is shown in the figure. Let A(x) = β«βΛ£ Ζ(t) dt and F(x) = β«βΛ£ Ζ(t) dt be two area functions for Ζ. Evaluate the following area functions.
(d) F(8)
Problem 5.3.14g
Area functions The graph of Ζ is shown in the figure. Let A(x) = β«βΛ£ Ζ(t) dt and F(x) = β«βΛ£ Ζ(t) dt be two area functions for Ζ. Evaluate the following area functions.
(g) F(2)
Problem 5.3.51c
Properties of integrals Use only the fact that β«ββ΄ 3π (4 βπ) dπ = 32, and the definitions and properties of integrals, to evaluate the following integrals, if possible.
(c) β«ββ° 6π(4 β π) d(π)
Problem 5.3.51d
Properties of integrals Use only the fact that β«ββ΄ 3π (4 βπ) dπ = 32, and the definitions and properties of integrals, to evaluate the following integrals, if possible.
(d) β«ββΈ 3π(4 β π) d(π)
Problem 5.3.85
Derivatives of integrals Simplify the following expressions.
d/dπ β«βΛ£ (β1 + tΒ²) dt (Hint: β«Λ£ββ (β1 + tΒ²) dt = β«β°ββ (β1 + tΒ²) dt + β«Λ£ββ (β1 + tΒ²) dt ) .
Problem 5.3.87a
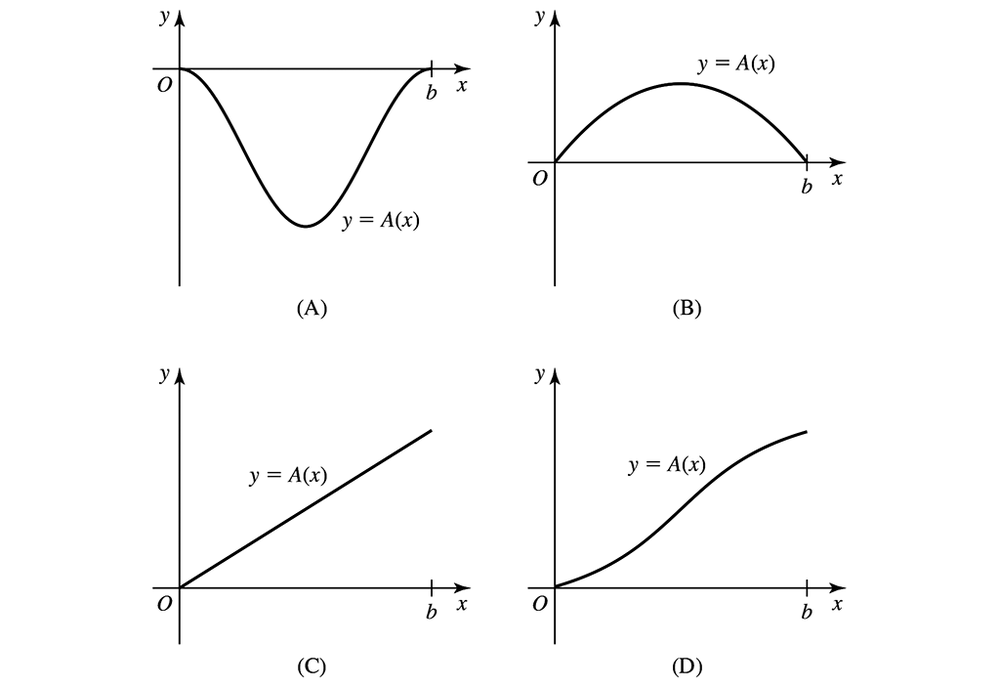
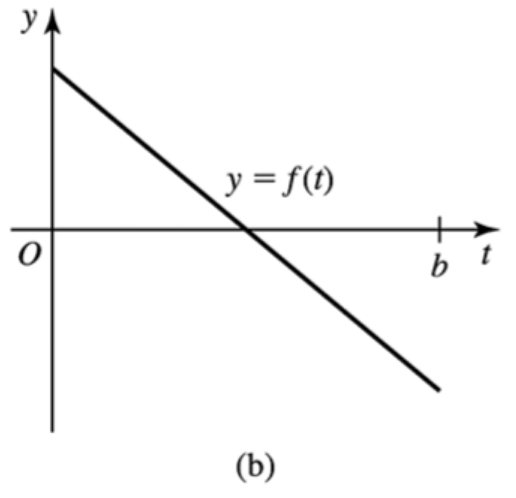
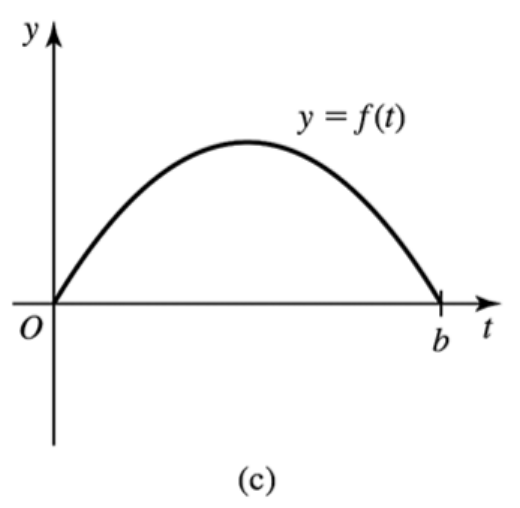
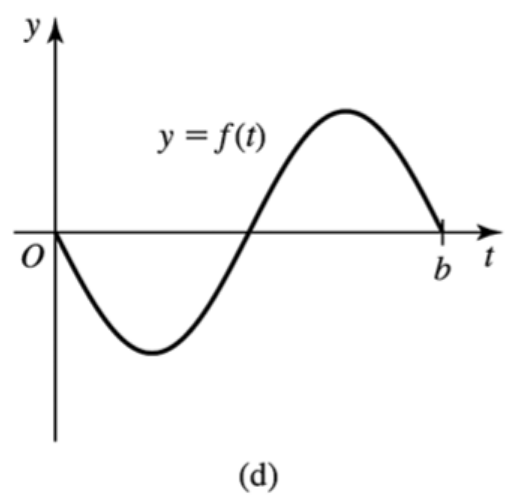
Matching functions with area functions Match the functions Ζ, whose graphs are given in aβ d, with the area functions A (π) = β«βΛ£ Ζ(t) dt, whose graphs are given in AβD.
Problem 5.3.87b
Matching functions with area functions Match the functions Ζ, whose graphs are given in aβ d, with the area functions A (π) = β«βΛ£ Ζ(t) dt, whose graphs are given in AβD.
Problem 5.3.87c
Matching functions with area functions Match the functions Ζ, whose graphs are given in aβ d, with the area functions A (π) = β«βΛ£ Ζ(t) dt, whose graphs are given in AβD.
Problem 5.3.87d
Matching functions with area functions Match the functions Ζ, whose graphs are given in aβ d, with the area functions A (π) = β«βΛ£ Ζ(t) dt, whose graphs are given in AβD.
Problem 5.3.2
Suppose F is an antiderivative of Ζ and A is an area function of Ζ. What is the relationship between F and A?
Problem 5.3.4
Let Ζ(π) = c, where c is a positive constant. Explain why an area function of Ζ is an increasing function.
Problem 5.3.6
Evaluate β«βΒ² 3πΒ² dπ and β«ββΒ² 3πΒ² dπ.
Problem 5.3.8
Why can the constant of integration be omitted from the antiderivative when evaluating a definite integral?
Problem 5.3.10
Explain why β«βα΅ Ζ β²(π) dπ = Ζ(b) β Ζ(a)
Problem 5.3.11
Evaluate β«ββΈ Ζ β²(t) dt , where Ζ β² is continuous on [3, 8], Ζ(3) = 4, and Ζ(8) = 20 .
Problem 5.3.94a
Working with area functions Consider the function Ζ and the points a, b, and c.
(a) Find the area function A (π) = β«βΛ£ Ζ(t) dt using the Fundamental Theorem.
Ζ(π) = sin π ; a = 0 , b = Ο/2 , c = Ο
Problem 5.3.95b
Working with area functions Consider the function Ζ and the points a, b, and c.
(b) Graph Ζ and A.
Ζ(π) = eΛ£ ; a = 0 , b = ln 2 , c = ln 4
Problem 5.3.96a
Working with area functions Consider the function Ζ and the points a, b, and c.
(a) Find the area function A (π) = β«βΛ£ Ζ(t) dt using the Fundamental Theorem.
Ζ(π) = β 12π (πβ1) (πβ 2) ; a = 0 , b = 1 , c = 2
Problem 5.3.96c
Working with area functions Consider the function Ζ and the points a, b, and c.
(c) Evaluate A(b) and A(c). Interpret the results using the graphs of part (b) .
Ζ(π) = β 12π (πβ1) (πβ 2) ; a = 0 , b = 1 , c = 2
Problem 5.3.97a
Working with area functions Consider the function Ζ and the points a, b, and c.
(a) Find the area function A (π) = β«βΛ£ Ζ(t) dt using the Fundamental Theorem.
Ζ(π) = cos π ; a = 0 , b = Ο/2 , c = Ο
Problem 5.3.98b
Working with area functions Consider the function Ζ and the points a, b, and c.
(b) Graph Ζ and A.
Ζ(π) = 1/π ; a = 1 , b = 4 , c = 6
