79–82. {Use of Tech} Double table look-up The following integrals may require more than one table look-up. Evaluate the integrals using a table of integrals, and then check your answer with a computer algebra system.

82. ∫ (sin⁻¹(ax)) / x² dx, a > 0

41–48. Geometry problems Use a table of integrals to solve the following problems.

43. Find the length of the curve y = eˣ on the interval from 0 to ln 2.

Arc length of a parabola Let L(c) be the length of the parabola f(x) = x² from x = 0 to x = c, where c ≥ 0 is a constant.

a. Find an expression for L.

Let L(c) be the length of the parabola f(x) = x² from x = 0 to x = c, where c ≥ 0 is a constant.

b. Is L concave up or concave down on [0, ∞)?

41–48. Geometry problems Use a table of integrals to solve the following problems.

42. Find the length of the curve y = x^(3/2) + 8 on the interval from 0 to 2.

11-14. {Use of Tech} Compute the absolute and relative errors in using c to approximate x.

12. x = √2; c = 1.414

3. Explain geometrically how the Trapezoid Rule is used to approximate a definite integral.

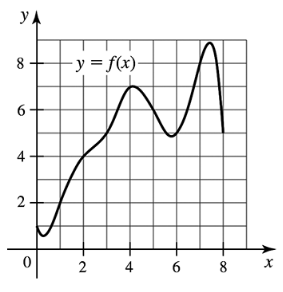
5-8. Compute the following estimates of ∫(0 to 8) f(x) dx using the graph in the figure.

6. T(4)

9. If the Trapezoid Rule is used on the interval [-1, 9] with n = 5 subintervals, at what x-coordinates is the integrand evaluated?

15-18. {Use of Tech} Midpoint Rule approximations. Find the indicated Midpoint Rule approximations to the following integrals.

15. ∫(2 to 10) 2x² dx using n = 1, 2, and 4 subintervals

15-18. {Use of Tech} Midpoint Rule approximations. Find the indicated Midpoint Rule approximations to the following integrals.

18. ∫(0 to 1) e⁻ˣ dx using n = 8 subintervals

19-22. {Use of Tech} Trapezoid Rule approximations. Find the indicated Trapezoid Rule approximations to the following integrals.

21. ∫(0 to 1) sin(πx) dx using n = 6 subintervals

23-26. {Use of Tech} Simpson's Rule approximations. Find the indicated Simpson's Rule approximations to the following integrals.

24. ∫(4 to 8) √x dx using n = 4 and n = 8 subintervals

27. {Use of Tech} Midpoint Rule, Trapezoid Rule, and relative error

Find the Midpoint and Trapezoid Rule approximations to ∫(0 to 1) sin(πx) dx using n = 25 subintervals. Compute the relative error of each approximation.

29-34. {Use of Tech} Comparing the Midpoint and Trapezoid Rules

Apply the Midpoint and Trapezoid Rules to the following integrals. Make a table similar to Table 8.5 showing the approximations and errors for n = 4, 8, 16, and 32. The exact values of the integrals are given for computing the error.

30. ∫(0 to 6) (x³/16 - x) dx = 4

29-34. {Use of Tech} Comparing the Midpoint and Trapezoid Rules

Apply the Midpoint and Trapezoid Rules to the following integrals. Make a table similar to Table 8.5 showing the approximations and errors for n = 4, 8, 16, and 32. The exact values of the integrals are given for computing the error.

33. ∫(0 to π) sin x cos(3x) dx = 0

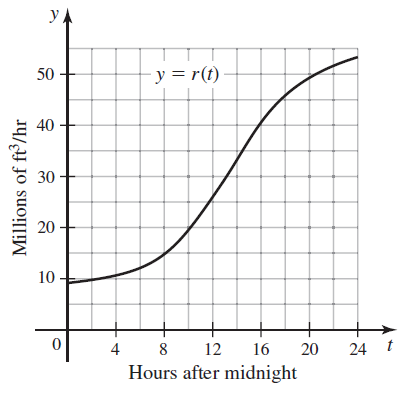
River flow rates

The following figure shows the discharge rate r(t) of the Snoqualmie River near Carnation, Washington, starting on a February day when the air temperature was rising. The variable t is the number of hours after midnight, r(t) is given in millions of cubic feet per hour, and ∫(0 to 24) r(t) dt equals the total amount of water that flows by the town of Carnation over a 24-hour period. Estimate ∫(0 to 24) r(t) dt using the Trapezoidal Rule and Simpson's Rule with the following values of n.

n = 6

41-44. {Use of Tech} Nonuniform grids

Use the indicated methods to solve the following problems with nonuniform grids.

41. A curling iron is plugged into an outlet at time t = 0. Its temperature T in degrees Fahrenheit, assumed to be a continuous function that is strictly increasing and concave down on 0 ≤ t ≤ 120, is given at various times (in seconds) in the table.

a. Approximate (1/120)∫(0 to 120)T(t)dt in three ways using a left Riemann sum, using a right Riemann sum and using the Trapezoid Rule

Interpret the value of (1/120)∫(0 to 120)T(t)dt in the context of this problem.

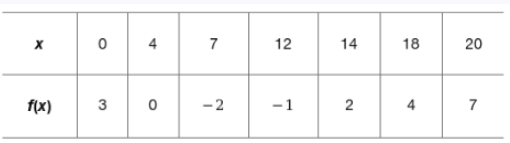
42. Approximating integrals The function f is twice differentiable on (-∞, ∞). Values of f at various points on [0, 20] are given in the table.

a. Approximate ∫(0 to 120) f(x) dx in three way using a left Riemann sum, a right Riemann sum and the Trapezoid Rule

43. A hot-air balloon is launched from an elevation of 5400 ft above sea level. As it rises, the vertical velocity is computed using a device (called a variometer) that measures the change in atmospheric pressure. The vertical velocities at selected times are shown in the table (with units of ft/min).​​

c. A polynomial that fits the data reasonably well is:

g(t) = 3.49t³ - 43.21t² + 142.43t - 1.75

Estimate the elevation of the balloon after five minutes using this polynomial.

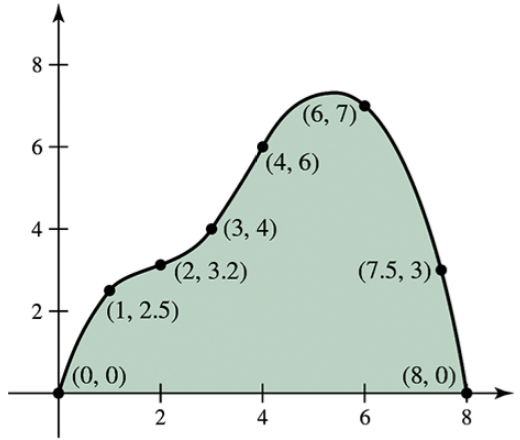
A piece of wood paneling must be cut in the shape shown in the figure.

The coordinates of several points on its curved surface are also shown (with units of inches).

a. Estimate the surface area of the paneling using the Trapezoid Rule.

45–48. {Use of Tech} Trapezoid Rule and Simpson’s Rule Consider the following integrals and the given values of n.

45. ∫(0 to 1) e^(2x) dx; n = 25

c. Compute the absolute errors in the Trapezoid Rule and Simpson’s Rule with 2n subintervals.

45–48. {Use of Tech} Trapezoid Rule and Simpson’s Rule Consider the following integrals and the given values of n.

46. ∫(0 to 2) x⁴ dx; n = 30

c. Compute the absolute errors in the Trapezoid Rule and Simpson’s Rule with 2n subintervals.

45–48. {Use of Tech} Trapezoid Rule and Simpson’s Rule Consider the following integrals and the given values of n.

47. ∫(1 to e) (1/x) dx; n = 50

c. Compute the absolute errors in the Trapezoid Rule and Simpson’s Rule with 2n subintervals.

45–48. {Use of Tech} Trapezoid Rule and Simpson’s Rule Consider the following integrals and the given values of n.

48. ∫(0 to π/4) (1/(1 + x²)) dx; n = 64

c. Compute the absolute errors in the Trapezoid Rule and Simpson’s Rule with 2n subintervals.

49–52. {Use of Tech} Simpson’s Rule

Apply Simpson’s Rule to the following integrals. It is easiest to obtain the Simpson’s Rule approximations from the Trapezoid Rule approximations, as in Example 8. Make a table similar to Table 8.8 showing the approximations and errors for n = 4, 8, 16, and 32. The exact values of the integrals are given for computing the error.

51. ∫(from 0 to π) e⁻ᵗ sin(t) dt = ½(e⁻ᵖⁱ + 1)

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

a. Suppose ∫_a^b f(x) dx is approximated with Simpson’s Rule using n = 18 subintervals, where |f^(4)(x)| ≤ 1 on [a, b]. The absolute error E_S in approximating the integral satisfies E_S ≤ (Δx)^5 / 10.

54–57. {Use of Tech} Comparing the Midpoint and Trapezoid Rules Compare the errors in the Midpoint and Trapezoid Rules with n = 4, 8, 16, and 32 subintervals when they are applied to the following integrals (with their exact values given).

54. ∫(from 0 to π/2) sin⁶x dx = 5π/32

54–57. {Use of Tech} Comparing the Midpoint and Trapezoid Rules Compare the errors in the Midpoint and Trapezoid Rules with n = 4, 8, 16, and 32 subintervals when they are applied to the following integrals (with their exact values given).

59. ∫(from 0 to π) ln(5 + 3cosx) dx = π ln(9/2)

58–61. {Use of Tech} Using Simpson's Rule Approximate the following integrals using Simpson's Rule. Experiment with values of n to ensure the error is less than 10⁻³.

60. ∫(from 0 to π) ln(2 + cos x) dx = π ln((2 + √3)/2)