Back
BackProblem 8.8.63
63. (Use of Tech) Normal distribution of heights
The heights of U.S. men are normally distributed with a mean of 69 in and a standard deviation of 3 in. This means that the fraction of men with a height between a and b (with a < b) inches is given by the integral
(1/(3√(2π))) ∫ₐᵇ e^(-((x-69)/3)²/2) dx.
What percentage of American men are between 66 and 72 inches tall? Use the method of your choice, and experiment with the number of subintervals until you obtain successive approximations that differ by less than 10⁻³.
Problem 8.8.64
64. (Use of Tech) Normal distribution of movie lengths
A study revealed that the lengths of U.S. movies are normally distributed with a mean of 110 minutes and a standard deviation of 22 minutes. This means that the fraction of movies with lengths between a and b minutes (with a < b) is given by the integral:
(1/(22√(2π))) ∫[a to b] e^(-((x-110)/22)²/2) dx.
What percentage of U.S. movies are between 1 hr and 1.5 hr long (60-90 min)?
Problem 8.8.66a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
66. Let f(x) = cos(x²).
a. Find a Midpoint Rule approximation to ∫[-1 to 1] cos(x²) dx using n = 30 subintervals.
Problem 8.8.66d
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
66. Let f(x) = cos(x²).
d. Use Theorem 8.1 to find an upper bound on the absolute error in the estimate found in part (a).
Problem 8.8.67a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
67. Let f(x) = √(x³ + 1).
a. Find a Midpoint Rule approximation to ∫[1 to 6] √(x³ + 1) dx using n = 50 subintervals.
Problem 8.8.67d
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
67. Let f(x) = √(x³ + 1).
d. Use Theorem 8.1 to find an upper bound on the absolute error in the estimate found in part (a).
Problem 8.8.68a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
68. Let f(x) = e^(x²).
a. Find a Trapezoid Rule approximation to ∫[0 to 1] e^(x²) dx using n = 50 subintervals.
Problem 8.8.68d
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
68. Let f(x) = e^(x²).
d. Use Theorem 8.1 to find an upper bound on the absolute error in the estimate found in part (a).
Problem 8.8.69a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
69. Let f(x) = sin(eˣ).
a. Find a Trapezoid Rule approximation to ∫[0 to 1] sin(eˣ) dx using n = 40 subintervals.
Problem 8.8.69d
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
69. Let f(x) = sin(eˣ).
d. Find an upper bound on the absolute error in the estimate found in part (a) using Theorem 8.1.
Problem 8.8.70a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
70. Let f(x) = e^(-x²).
a. Find a Simpson's Rule approximation to the integral from 0 to 3 of e^(-x²) dx using n = 30 subintervals.
Problem 8.8.71a
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
71. Let f(x) = √(sin x).
a. Find a Simpson's Rule approximation to the integral from 1 to 2 of √(sin x) dx using n = 20 subintervals.
Problem 8.8.71b
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
71. Let f(x) = √(sin x).
b. Find an upper bound on the absolute error in the estimate from part (a) using Theorem 8.1. (Hint: |f''''(x)| ≤ 1 on [1,2].)
Problem 8.8.66b
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
66. Let f(x) = cos(x²).
b. Calculate f''(x).
Problem 8.8.67b
66–71. {Use of Tech} Estimating error Refer to Theorem 8.1 in the following exercises.
67. Let f(x) = √(x³ + 1).
b. Calculate f''(x).
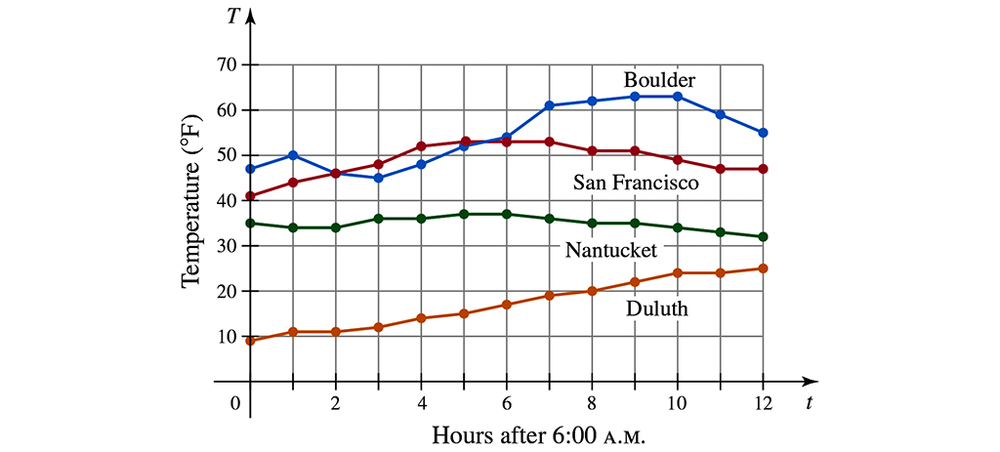
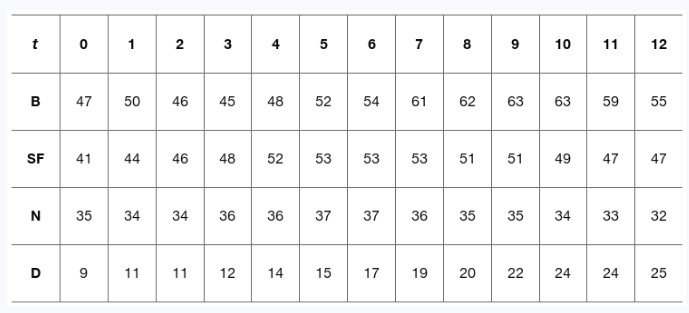
Problem 8.8.38
37-40. {Use of Tech} Temperature data
Howdy temperature data for Boulder, Colorado; San Francisco, California; Nantucket, Massachusetts; and Duluth, Minnesota, over a 12-hr period on the same day of January are shown in the figure.
Assume these data are taken from a continuous temperature function T(t). The average temperature (in °F) over the 12-hr period is:
T_avg = (1/12) × ∫(0 to 12) T(t) dt
38. Find an accurate approximation to the average temperature over the 12-hr period for San Francisco. State your method.
Problem 8.87b
{Use of Tech} Powers of sine and cosine It can be shown that
∫ from 0 to π/2 of sinⁿx dx = ∫ from 0 to π/2 of cosⁿx dx =
{
[1·3·5···(n-1)]/[2·4·6···n] · π/2 if n ≥ 2 is even
[2·4·6···(n-1)]/[3·5···n] if n ≥ 3 is odd
}
b. Evaluate the integrals with n = 10 and confirm the result.
Problem 8.9.4
4. Evaluate ∫ (from 0 to 1) (1/x^(1/5)) dx after writing the integral as a limit.
Problem 8.9.7
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
10. ∫ (from 0 to ∞) e⁻²ˣ dx
Problem 8.9.10
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
10. ∫ (from 0 to ∞) e⁻²ˣ dx
Problem 8.9.13
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
13. ∫ (from 0 to ∞) cos x dx
Problem 8.9.16
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
16. ∫ (from -∞ to ∞) (1/(x² + a²)) dx, a > 0
Problem 8.9.19
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
19. ∫ (from 1 to ∞) (3x² + 1)/(x³ + x) dx
Problem 8.9.22
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
22. ∫ (from -∞ to -2) (1/x²) sin(π/2) dx
Problem 8.9.25
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
25. ∫ (from -∞ to ∞) e³ˣ/(1 + e⁶ˣ) dx
Problem 8.9.33
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
33. ∫ (from 2 to ∞) 1/(y ln y) dy
Problem 8.9.36
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
36. ∫ (from e² to ∞) 1/(x lnᵖ x) dx, p > 1
Problem 8.9.39
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
39. ∫ (from 0 to π/2) tan θ dθ
Problem 8.9.42
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
42. ∫ (from 3 to 4) 1/(x-3)³ᐟ² dx
Problem 8.9.44
7–58. Improper integrals Evaluate the following integrals or state that they diverge.
44. ∫ (from 0 to ln 3) eʸ/(eʸ-1)⁷ᐟ³ dy