Back
BackProblem 8.3.74
74. A secant reduction formula
Prove that for positive integers n ≠ 1,
∫ secⁿ x dx = (secⁿ⁻² x tan x)/(n − 1) + (n − 2)/(n − 1) ∫ secⁿ⁻² x dx.
(Hint: Integrate by parts with u = secⁿ⁻² x and dv = sec² x dx.)
Problem 8.3.75c
75. Exploring powers of sine and cosine
c. Prove that ∫₀ᵖⁱ sin²(nx) dx has the same value for all positive integers n.
Problem 8.3.75e
75. Exploring powers of sine and cosine
e. Repeat parts (a), (b), and (c) with sin²x replaced by sin⁴x. Comment on your observations.
Problem 8.3.1
1. State the half-angle identities used to integrate sin²x and cos²x.
Problem 8.3.10
9–61. Trigonometric integrals Evaluate the following integrals.
10. ∫ sin³x dx
Problem 8.3.11
9–61. Trigonometric integrals Evaluate the following integrals.
11. ∫ sin²(3x) dx
Problem 8.3.13
9–61. Trigonometric integrals Evaluate the following integrals.
13. ∫ sin⁵x dx
Problem 8.3.15
9–61. Trigonometric integrals Evaluate the following integrals.
15. ∫ sin³x cos²x dx
Problem 8.3.16
9–61. Trigonometric integrals Evaluate the following integrals.
16. ∫ sin²θ cos⁵θ dθ
Problem 8.3.19
9–61. Trigonometric integrals Evaluate the following integrals.
19. ∫[0 to π/3] sin⁵x cos⁻²x dx
Problem 8.3.20
9–61. Trigonometric integrals Evaluate the following integrals.
20. ∫ sin⁻³ᐟ²x cos³x dx
Problem 8.3.22
9–61. Trigonometric integrals Evaluate the following integrals.
22. ∫[π/4 to π/2] sin²(2x) cos³(2x) dx
Problem 8.3.26
9–61. Trigonometric integrals Evaluate the following integrals.
26. ∫ sin³x cos³ᐟ²x dx
Problem 8.3.25
9–61. Trigonometric integrals Evaluate the following integrals.
25. ∫ sin²x cos⁴x dx
Problem 8.3.28
9–61. Trigonometric integrals Evaluate the following integrals.
28. ∫ 6 sec⁴x dx
Problem 8.3.63a
63. Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
a. If m is a positive integer, then ∫[0 to π] cos^(2m+1)(x) dx = 0.
Problem 8.3.63b
63. Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
b. If m is a positive integer, then ∫[0 to π] sin^m(x) dx = 0.
Problem 8.4.16
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
16. ∫ x²/(25 + x²)² dx
Problem 8.4.19
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
19. ∫ 1/√(x² - 81) dx, x > 9
Problem 8.4.23
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
23. ∫ 1/(25 - x²)^(3/2) dx
Problem 8.4.26
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
26. ∫[√2 to √2] √(x² - 1)/x dx
Problem 8.4.30
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
30. ∫ x³√(1 - x²) dx
Problem 8.4.33
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
33. ∫ √(x² - 9)/x dx, x > 3
Problem 8.4.36
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
36. ∫[8√2 to 16] 1/√(x² - 64) dx
Problem 8.4.39
7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.
39. ∫ x²/(100 - x²)^(3/2) dx
Problem 8.4.68
60–69. Completing the square Evaluate the following integrals.
68. ∫ dx / sqrt((x - 1)(3 - x))
Problem 8.4.65
60–69. Completing the square Evaluate the following integrals.
65. ∫[1/2 to (√2 + 3)/(2√2)] dx / (8x² - 8x + 11)
Problem 8.4.62
60–69. Completing the square Evaluate the following integrals.
62. ∫ du / (2u² - 12u + 36)
Problem 8.4.59
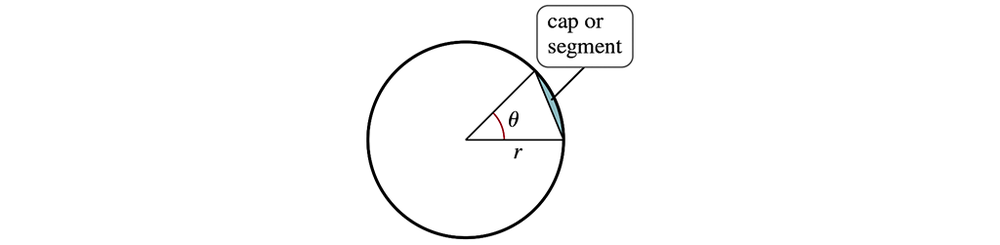
59. Area of a segment of a circle
Use two approaches to show that the area of a cap (or segment) of a circle of radius r subtended by an angle θ (see figure) is given by:
A_seg = (1/2) r² (θ - sin θ)
b. Find the area using calculus.
Problem 8.4.57d
57. Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
d. The integral ∫ dx/(x² + 4x + 9) cannot be evaluated using a trigonometric substitution.