Back
BackProblem 8.2.81a
81. Possible and impossible integrals
Let Iₙ = ∫ xⁿ e⁻ˣ² dx, where n is a nonnegative integer.
a. I₀ = ∫ e⁻ˣ² dx cannot be expressed in terms of elementary functions. Evaluate I₁.
Problem 8.2.81d
81. Possible and impossible integrals
Let Iₙ = ∫ xⁿ e⁻ˣ² dx, where n is a nonnegative integer.
d. Show that, in general, if n is odd, then Iₙ = -½ e⁻ˣ² pₙ₋₁(x), where pₙ₋₁ is a polynomial of degree n - 1.
Problem 8.2.82b
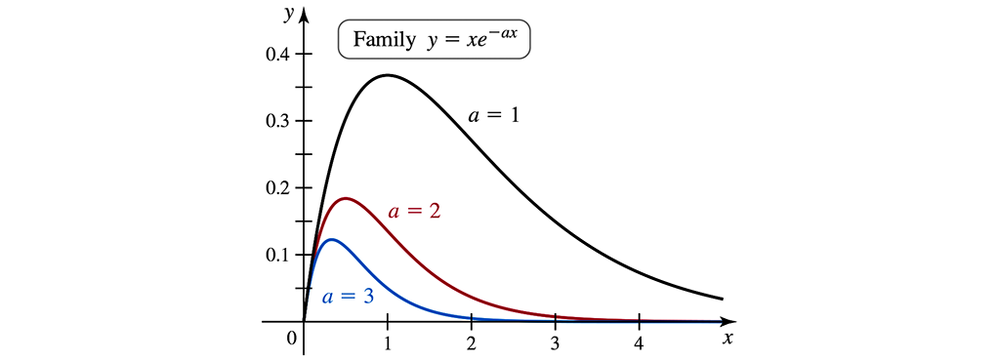
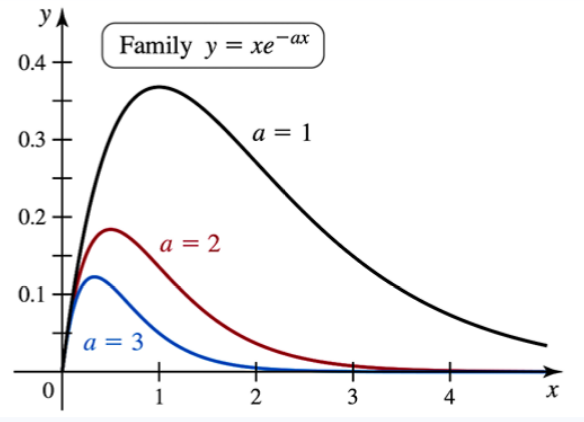
82. A family of exponentials The curves y = x * e^(-a * x) are shown in the figure for a = 1, 2, and 3.
b. Find the area of the region bounded by y = x * e^(-a * x) and the x-axis on the interval [0, 4], where a > 0.
Problem 8.2.82c
82. A family of exponentials The curves y = x * e^(-a * x) are shown in the figure for a = 1, 2, and 3.
c. Find the area of the region bounded by y = x * e^(-a * x) and the x-axis on the interval [0, b]. Because this area depends on a and b, we call it A(a, b).
Problem 8.2.75a
75. {Use of Tech} Oscillator displacements Suppose a mass on a spring that is slowed by friction has the position function:
s(t) = e⁻ᵗ sin t
a. Graph the position function. At what times does the oscillator pass through the position s = 0?
Problem 8.2.78b
Practice with tabular integration Evaluate the following integrals using tabular integration (refer to Exercise 77).
b. ∫ 7x e³ˣ dx
Problem 8.2.82e
82. A family of exponentials The curves y = x * e^(-a * x) are shown in the figure for a = 1, 2, and 3.
e. Does this pattern continue? Is it true that A(1, ln b) = a² * A(a, (ln b)/a)?
Problem 8.2.75c
75. {Use of Tech} Oscillator displacements Suppose a mass on a spring that is slowed by friction has the position function:
s(t) = e⁻ᵗ sin t
c. Generalize part (b) and find the average value of the position on the interval [nπ, (n+1)π], for n = 0, 1, 2, ...
Problem 8.3.47
9–61. Trigonometric integrals Evaluate the following integrals.
47. ∫ (csc⁴x)/(cot²x) dx
Problem 8.3.3
3. Describe the method used to integrate sin³x.
Problem 8.3.4
4. Describe the method used to integrate sinᵐx cosⁿx, for m even and n odd.
Problem 8.3.5
5. What is a reduction formula?
Problem 8.3.7
7. How would you evaluate ∫ tan¹⁰x sec²x dx?
Problem 8.3.31
9–61. Trigonometric integrals Evaluate the following integrals.
31. ∫ 20 tan⁶x dx
Problem 8.3.34
9–61. Trigonometric integrals Evaluate the following integrals.
34. ∫ tan⁹x sec⁴x dx
Problem 8.3.37
9–61. Trigonometric integrals Evaluate the following integrals.
37. ∫ [sec⁴(lnθ)]/θ dθ
Problem 8.3.38
9–61. Trigonometric integrals Evaluate the following integrals.
38. ∫ tan⁵θ sec⁴θ dθ
Problem 8.3.43
9–61. Trigonometric integrals Evaluate the following integrals.
43. ∫ tan³(4x) dx
Problem 8.3.45
9–61. Trigonometric integrals Evaluate the following integrals.
45. ∫ sec²x tan¹ᐟ²x dx
Problem 8.3.50
9–61. Trigonometric integrals Evaluate the following integrals.
50. ∫ csc¹⁰x cot³x dx
Problem 8.3.51
9–61. Trigonometric integrals Evaluate the following integrals.
51. ∫ (csc²x + csc⁴x) dx
Problem 8.3.53
9–61. Trigonometric integrals Evaluate the following integrals.
53. ∫ from 0 to π/4 of sec⁴θ dθ
Problem 8.3.59
9–61. Trigonometric integrals Evaluate the following integrals.
59. ∫ from 0 to π/2 of √(1 - cos2x) dx
Problem 8.3.60
9–61. Trigonometric integrals Evaluate the following integrals.
60. ∫ from 0 to π/8 of √(1 - cos8x) dx
Problem 8.3.40
9–61. Trigonometric integrals Evaluate the following integrals.
40. ∫[0 to π/6] tan⁵(2x) sec(2x) dx
Problem 8.3.57
9–61. Trigonometric integrals Evaluate the following integrals.
57. ∫ from 0 to π of (1 - cos2x)³ᐟ² dx
Problem 8.3.65
65. Volume Find the volume of the solid generated when the region bounded by y = sin²(x) * cos^(3/2)(x) and the x-axis on the interval [0, π/2] is revolved about the x-axis.
Problem 8.3.68
67-70. Integrals of the form ∫ sin(mx)cos(nx) dx Use the following product-to-sum identities to evaluate the given integrals:
sin(mx)sin(nx) = ½[cos((m-n)x) - cos((m+n)x)]
sin(mx)cos(nx) = ½[sin((m-n)x) + sin((m+n)x)]
cos(mx)cos(nx) = ½[cos((m-n)x) + cos((m+n)x)]
68. ∫ sin(5x)sin(7x) dx
Problem 8.3.70
67-70. Integrals of the form ∫ sin(mx)cos(nx) dx Use the following product-to-sum identities to evaluate the given integrals:
sin(mx)sin(nx) = ½[cos((m-n)x) - cos((m+n)x)]
sin(mx)cos(nx) = ½[sin((m-n)x) + sin((m+n)x)]
cos(mx)cos(nx) = ½[cos((m-n)x) + cos((m+n)x)]
70. ∫ cos(x)cos(2x) dx
Problem 8.3.71c
Prove the following orthogonality relations (which are used to generate Fourier series). Assume m and n are integers with m ≠ n.
c.
π
∫ sin(mx) cos(nx) dx = 0, when |m + n| is even
0

![Graph showing three curves of y = x * e^(-a * x) for a = 1, 2, and 3, decreasing and approaching zero on [0,4].](https://static.studychannel.pearsonprd.tech/courses/calculus/thumbnails/a3b793f9-f31f-40a3-a153-ba6be7b8c3a3)