57. Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

a. If x = 4 tanθ, then cscθ = 4/x.

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

54. ∫ y⁴/(1 + y²) dy

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

51. ∫ x²/√(4 + x²) dx

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

48. ∫ √(9 - 4x²) dx

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

46. ∫ 1/√(1 - 2x²) dx

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

44. ∫ 1/√(16 + 4x²) dx

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

42. ∫ 1/(x²√(9x² - 1)) dx, x > 1/3

2. What change of variables is suggested by an integral containing √(x² + 36)?

6. Using the trigonometric substitution x = 8 sec θ, where x ≥ 8 and 0 < θ ≤ π/2, express tan θ in terms of x.

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

9. ∫[5 to 5√3] √(100 - x²) dx

7-56. Trigonometric substitutions Evaluate the following integrals using trigonometric substitution.

12. ∫[1/2 to 1] √(1 - x²)/x² dx

Clever substitution Evaluate ∫ dx/(1 + sin x + cos x) using the substitution x=2 tan⁻¹ θ. The identities sin x = 2 sin(x/2) cos(x/2) and cos x =cos²(x/2) − sin²(x/2) are helpful.

Area and volume Consider the function f(x) = (9 + x²)^(-1/2) and the region R on the interval [0, 4] (see figure).

b. Find the volume of the solid generated when R is revolved about the x-axis.

Computing areas On the interval [0,2], the graphs of f(x)=x²/3 and g(x)=x²(9−x²)^(-1/2) have similar shapes.

a. Find the area of the region bounded by the graph of f and the x-axis on the interval [0,2].

Computing areas On the interval [0,2], the graphs of f(x)=x²/3 and g(x)=x²(9−x²)^(-1/2) have similar shapes.

b. Find the area of the region bounded by the graph of g and the x-axis on the interval [0,2].

Computing areas On the interval [0,2], the graphs of f(x)=x²/3 and g(x)=x²(9−x²)^(-1/2) have similar shapes.

c. Which region has greater area?

{Use of Tech} Using the integral of sec³u By reduction formula 4 in Section 8.3,

∫sec³u du = 1/2 (sec u tan u + ln |sec u + tan u|) + C

Graph the following functions and find the area under the curve on the given interval.

f(x) = 1/(x√(x² - 36)), [12/√3 , 12]

{Use of Tech} Using the integral of sec³u By reduction formula 4 in Section 8.3,

∫sec³u du = 1/2 (sec u tan u + ln |sec u + tan u|) + C

Graph the following functions and find the area under the curve on the given interval.

f(x) = (9 - x²) ⁻², [0, 3/2]

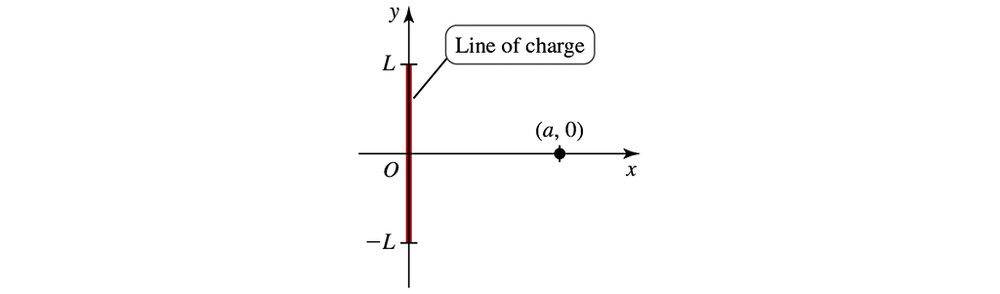
"Electric field due to a line of charge A total charge of Q is distributed uniformly on a line segment of length 2L along the y-axis (see figure). The x-component of the electric field at a point (a, 0) is given by

Eₓ(a) = (kQa/2L) ∫-L L dy/(a² + y²)^(3/2),

where k is a physical constant and a > 0.

a. Confirm that Eₓ(a)=kQ / a √(a²+L²)

b. Letting ρ=Q / 2 L be the charge density on the line segment, show that if L → ∞, then Eₓ(a) = 2kρ / a.

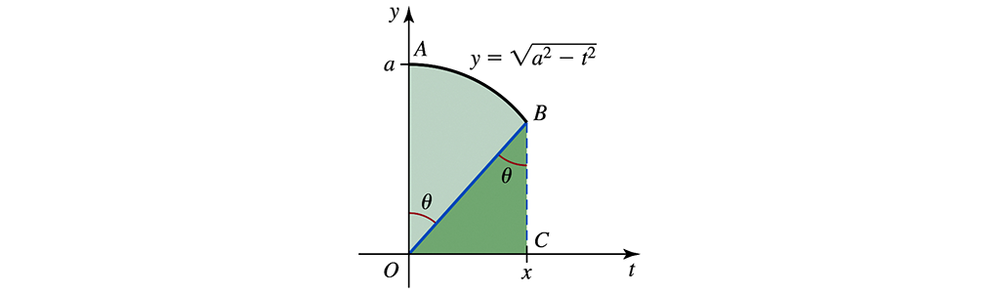
Visual proof Let F(x)=∫₀ˣ √(a²−t²) dt. The figure shows that F(x)= area of sector OAB+ area of triangle OBC.

a. Use the figure to prove that

F(x) = (a² sin ⁻¹(x/a))/2 + x√(a²−x²)/2

b. Conclude that ∫ √(a²−x²) dx = (a² sin ⁻¹(x/a))/2 + x√(a²−x²)/2 + C.

17-22. Give the partial fraction decomposition for the following expressions.

17. (5x - 7) / (x² - 3x + 2)

5–16. Set up the appropriate form of the partial fraction decomposition for the following expressions. Do not find the values of the unknown constants.

15. x / ((x⁴ - 16)²)

23-64. Integration Evaluate the following integrals.

23. ∫ [3 / ((x - 1)(x + 2))] dx

23-64. Integration Evaluate the following integrals.

26. ∫₀¹ [1 / (t² - 9)] dt

5–16. Set up the appropriate form of the partial fraction decomposition for the following expressions. Do not find the values of the unknown constants.

6. (4x + 1)/(4x² - 1)

5–16. Set up the appropriate form of the partial fraction decomposition for the following expressions. Do not find the values of the unknown constants.

9. 4/(x⁵ - 5x³ + 4x)

5–16. Set up the appropriate form of the partial fraction decomposition for the following expressions. Do not find the values of the unknown constants.

12. (2x² + 3)/((x² - 8x + 16)(x² + 3x + 4))

23-64. Integration Evaluate the following integrals.

29. ∫₋₁² [(5x) / (x² - x - 6)] dx

23-64. Integration Evaluate the following integrals.

32. ∫ (4x - 2)/(x³ - x) dx

23-64. Integration Evaluate the following integrals.

35. ∫ (x² + 12x - 4)/(x³ - 4x) dx