Back
BackProblem 9.5.1
Explain how the growth rate function determines the solution of a population model.
Problem 9.5.4
Explain how a stirred tank reaction works.
Problem 9.5.6
What are the assumptions underlying the predator-prey model discussed in this section?
Problem 9.5.13
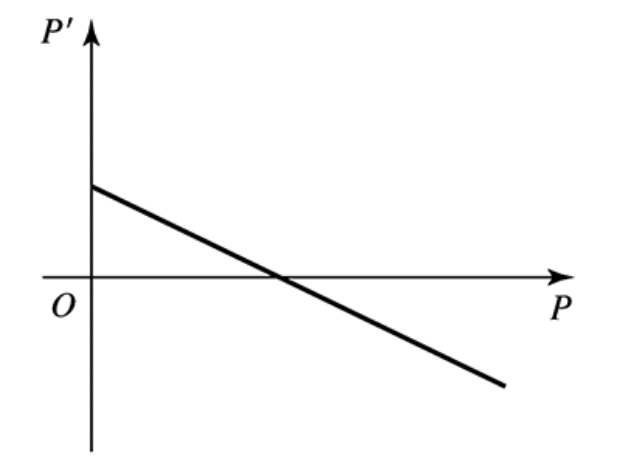
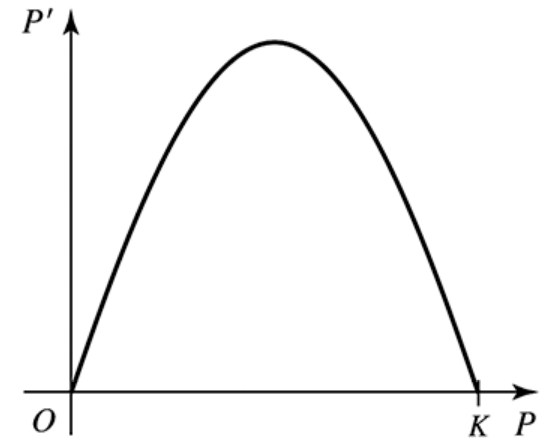
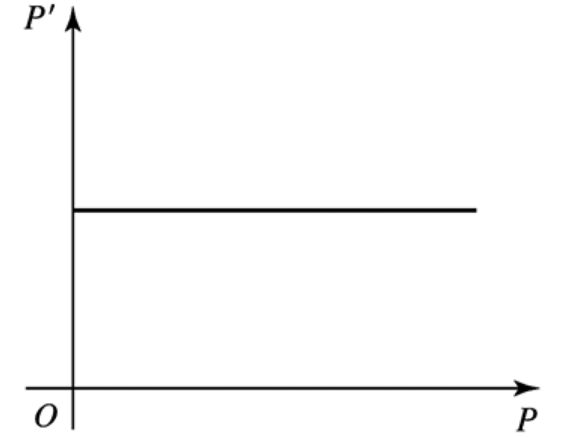
9–14. Growth rate functions Make a sketch of the population function P (as a function of time) that results from the following growth rate functions. Assume the population at time t = 0 begins at some positive value.
Problem 9.5.11
9–14. Growth rate functions Make a sketch of the population function P (as a function of time) that results from the following growth rate functions. Assume the population at time t = 0 begins at some positive value.
Problem 9.5.9
9–14. Growth rate functions Make a sketch of the population function P (as a function of time) that results from the following growth rate functions. Assume the population at time t = 0 begins at some positive value.
Problem 9.5.23a
23–26. Stirred tank reactions For each of the following stirred tank reactions, carry out the following analysis.
a. Write an initial value problem for the mass of the substance.
A 500-L tank is initially filled with pure water. A copper sulfate solution with a concentration of 20 g/L flows into the tank at a rate of 4 L/min. The thoroughly mixed solution is drained from the tank at a rate of 4 L/min.
Problem 9.5.23b
23–26. Stirred tank reactions For each of the following stirred tank reactions, carry out the following analysis.
b. Solve the initial value problem.
A 500-L tank is initially filled with pure water. A copper sulfate solution with a concentration of 20 g/L flows into the tank at a rate of 4 L/min. The thoroughly mixed solution is drained from the tank at a rate of 4 L/min.
Problem 9.5.26a
23–26. Stirred tank reactions For each of the following stirred tank reactions, carry out the following analysis.
a. Write an initial value problem for the mass of the substance.
A one-million-liter pond is contaminated by a chemical pollutant with a concentration of 20 g/L. The source of the pollutant is removed, and pure water is allowed to flow into the pond at a rate of 1200 L/hr. Assuming the pond is thoroughly mixed and drained at a rate of 1200 L/hr, how long does it take to reduce the concentration of the solution in the pond to 10% of the initial value?
Problem 9.5.26b
23–26. Stirred tank reactions For each of the following stirred tank reactions, carry out the following analysis.
b. Solve the initial value problem.
A one-million-liter pond is contaminated by a chemical pollutant with a concentration of 20 g/L. The source of the pollutant is removed, and pure water is allowed to flow into the pond at a rate of 1200 L/hr. Assuming the pond is thoroughly mixed and drained at a rate of 1200 L/hr, how long does it take to reduce the concentration of the solution in the pond to 10% of the initial value?
Problem 9.5.27c
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
c. Find the equilibrium points for the system.
x′(t) = −3x + 6xy, y′(t) = y − 4xy
Problem 9.5.28b
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
b. Find the lines along which x'(t) = 0. Find the lines along which y'(t) = 0.
x′(t) = 2x − 4xy, y′(t) = −y + 2xy
Problem 9.5.28d
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
d. Identify the four regions in the first quadrant of the xy-plane in which x' and y' are positive or negative.
x′(t) = 2x − 4xy, y′(t) = −y + 2xy
Problem 9.5.29a
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
a. Identify which equation corresponds to the predator and which corresponds to the prey.
x′(t) = −3x + xy, y′(t) = 2y − xy
Problem 9.5.29c
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
c. Find the equilibrium points for the system.
x′(t) = −3x + xy, y′(t) = 2y − xy
Problem 9.5.30b
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
b. Find the lines along which x'(t) = 0. Find the lines along which y'(t) = 0.
x′(t) = 2x − xy, y′(t) = −y + xy
Problem 9.5.15
15–16. {Use of Tech} Solving logistic equations Write a logistic equation with the following parameter values. Then solve the initial value problem and graph the solution. Let r be the natural growth rate, K the carrying capacity, and P₀ the initial population.
r=0.2, K=300, P₀=50
Problem 9.5.31b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
b. The solution of a stirred tank initial value problem always approaches a constant as t→∞
Problem 9.5.32a
Growth rate functions
a. Show that the logistic growth rate function f(P)=rP(1−P/K) has a maximum value of rK/4 at the point P=K/2.
Problem 9.5.33
Solution of the logistic equation Use separation of variables to show that the solution of the initial value problem
P'(t) = rP (1-P/K), P(0) = P₀
is P(t) = K/((K/P₀ − 1)e⁻ʳᵗ + 1)
Problem 9.5.35b
Properties of stirred tank solutions
b. Verify that M(0) = M₀
Problem 9.5.36a
A physiological model A common assumption in modeling drug assimilation is that the blood volume in a person is a single compartment that behaves like a stirred tank. Suppose the blood volume is a four-liter tank that initially has a zero concentration of a particular drug. At time t = 0, an intravenous line is inserted into a vein (into the tank) that carries a drug solution with a concentration of 500 mg/L. The inflow rate is 0.06 L/min. Assume the drug is quickly mixed thoroughly in the blood and that the volume of blood remains constant.
a. Write an initial value problem that models the mass of the drug in the blood, for t ≥ 0.
Problem 9.5.36d
A physiological model A common assumption in modeling drug assimilation is that the blood volume in a person is a single compartment that behaves like a stirred tank. Suppose the blood volume is a four-liter tank that initially has a zero concentration of a particular drug. At time t = 0, an intravenous line is inserted into a vein (into the tank) that carries a drug solution with a concentration of 500 mg/L. The inflow rate is 0.06 L/min. Assume the drug is quickly mixed thoroughly in the blood and that the volume of blood remains constant.
d. After how many minutes does the drug mass reach 90% of its steady-state level?
Problem 9.5.38a
U.S. population projections According to the U.S. Census Bureau, the nation’s population (to the nearest million) was 296 million in 2005 and 321 million in 2015. The Bureau also projects a 2050 population of 398 million. To construct a logistic model, both the growth rate and the carrying capacity must be estimated. There are several ways to estimate these parameters. Here is one approach:
a. Assume t = 0 corresponds to 2005 and that the population growth is exponential for the first ten years; that is, between 2005 and 2015, the population is given by P(t) = P(0)exp(rt). Estimate the growth rate r using this assumption.
Problem 9.5.38d
U.S. population projections According to the U.S. Census Bureau, the nation’s population (to the nearest million) was 296 million in 2005 and 321 million in 2015. The Bureau also projects a 2050 population of 398 million. To construct a logistic model, both the growth rate and the carrying capacity must be estimated. There are several ways to estimate these parameters. Here is one approach:
d. Estimations of this kind must be made and interpreted carefully. Suppose the projected population for 2050 is 410 million rather than 398 million. What is the value of the carrying capacity in this case?
Problem 9.5.39a
{Use of Tech} Analytical solution of the predator-prey equations The solution of the predator-prey equations
X'(t) = -ax + bxy,y’(t) = cy - dxy
can be viewed as parametric equations that describe the solution curves. Assume a, b, c, and d are positive constants and consider solutions in the first quadrant.
a. Recalling that dy/dx = y(t)/x′(t), divide the first equation by the second equation to obtain a separable differential equation in terms of x and y.
Problem 9.5.18
17–18. {Use of Tech} Designing logistic functions Use the method of Example 1 to find a logistic function that describes the following populations. Graph the population function.
The population increases from 50 to 60 in the first month and eventually levels off at 150.
Problem 9.5.21
20–22. {Use of Tech} Solving the Gompertz equation Solve the Gompertz equation in Exercise 19 with the given values of r, K, and M₀. Then graph the solution to be sure that M(0) and lim(t→∞) M(t) are correct.
r = 0.05, K = 1200, M₀ = 90
Problem 9.5.27e
27–30. Predator-prey models Consider the following pairs of differential equations that model a predator-prey system with populations x and y. In each case, carry out the following steps.
e. Sketch a representative solution curve in the xy-plane and indicate the direction in which the solution evolves.
x′(t) = −3x + 6xy, y′(t) = y − 4xy