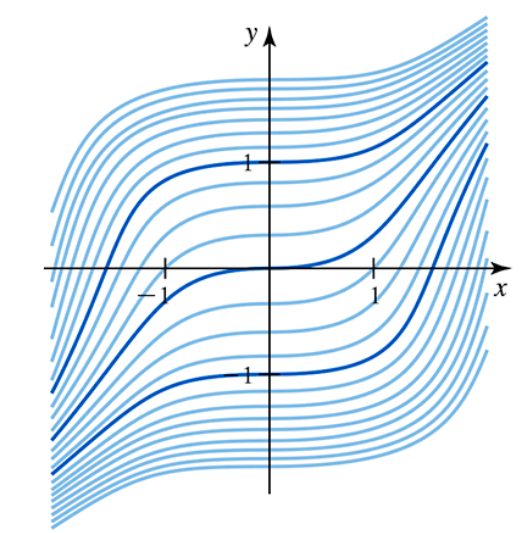
Direction field analysis Consider the first-order initial value problem y'(t)=ay+b, y(0)=A for t≥0 where a, b, and A are real numbers.

c. Draw a representative direction field in the case that a<0. Show that if A>−b/a, then the solution decreases for t≥0, and that if A<−b/a, then the solution increases for t≥0.

46–48. Analyzing models The following models were discussed in Section 9.1 and reappear in later sections of this chapter. In each case, carry out the indicated analysis using direction fields.

Drug infusion The delivery of a drug (such as an antibiotic) through an intravenous line may be modeled by the differential equation m′(t)+km(t)=I, where m(t) is the mass of the drug in the blood at time t≥0, K is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let I=10 mg/hr and k=0.05 hr^−1.

a. Draw the direction field, for 0≤t≤100, 0≤y≤600.

38–43. Equilibrium solutions A differential equation of the form y′(t)=f(y) is said to be autonomous (the function f depends only on y). The constant function y=y0 is an equilibrium solution of the equation provided f(y0)=0 (because then y'(t)=0 and the solution remains constant for all t). Note that equilibrium solutions correspond to horizontal lines in the direction field. Note also that for autonomous equations, the direction field is independent of t. Carry out the following analysis on the given equations.

b. Sketch the direction field, for t≥0. 

y′(t) = 6 - 2y

17–32. Solving initial value problems Determine whether the following equations are separable. If so, solve the initial value problem.

y'(t) = cos² y, y(1) = π/4

33–38. {Use of Tech} Solutions in implicit form Solve the following initial value problems and leave the solution in implicit form. Use graphing software to plot the solution. If the implicit solution describes more than one function, be sure to indicate which function corresponds to the solution of the initial value problem.

z(x) = (z² + 4)/(x² + 16), z(4) = 2

​​​​​​​​What is a separable first-order differential equation?

Explain how to solve a separable differential equation of the form

g(t)y'(y) = h(t)

5–16. Solving separable equations Find the general solution of the following equations. Express the solution explicitly as a function of the independent variable.

e⁴ᵗy'(t) = 5

5–16. Solving separable equations Find the general solution of the following equations. Express the solution explicitly as a function of the independent variable.

y'(t) = eʸᐟ²sin t

5–16. Solving separable equations Find the general solution of the following equations. Express the solution explicitly as a function of the independent variable.

(t² + 1)³yy'(t) = t(y² + 4)

5–16. Solving separable equations Find the general solution of the following equations. Express the solution explicitly as a function of the independent variable.

u'(x) = e²ˣ⁻ᵘ

17–32. Solving initial value problems Determine whether the following equations are separable. If so, solve the initial value problem.

y'(t) = eᵗʸ, y(0) = 1

17–32. Solving initial value problems Determine whether the following equations are separable. If so, solve the initial value problem.

y'(t) = yeᵗ, y(0) = −1

17–32. Solving initial value problems Determine whether the following equations are separable. If so, solve the initial value problem.

y(t) = sec² t/(2y), y(π/4) = 1

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

c. The general solution of the equation yy'(x) = xe⁻ʸ can be found using integration by parts.

17–32. Solving initial value problems Determine whether the following equations are separable. If so, solve the initial value problem.

y'(t) = y³sin t, y(0) = 1

33–38. {Use of Tech} Solutions in implicit form Solve the following initial value problems and leave the solution in implicit form. Use graphing software to plot the solution. If the implicit solution describes more than one function, be sure to indicate which function corresponds to the solution of the initial value problem.

yy'(x) = 2x/(2 + y)², y(1) = −1

33–38. {Use of Tech} Solutions in implicit form Solve the following initial value problems and leave the solution in implicit form. Use graphing software to plot the solution. If the implicit solution describes more than one function, be sure to indicate which function corresponds to the solution of the initial value problem.

y'(t) = 2t²/(y² − 1), y(0) = 0

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

b. The general solution of the separable equation y'(t) = t/(y' + 10y⁴) can be expressed explicitly with y in terms of t.

{Use of Tech} Logistic equation for an epidemic When an infected person is introduced into a closed and otherwise healthy community, the number of people who contract the disease (in the absence of any intervention) may be modeled by the logistic equation

dP/dt=kP(1−P/A),P0 =P_0,

where K is a positive infection rate, A is the number of people in the community, and P0 is the number of infected people at t=0. The model also assumes no recovery.

a. Find the solution of the initial value problem, for t≥0, in terms of K, A, and P0.

42–43. Implicit solutions for separable equations For the following separable equations, carry out the indicated analysis.

a. Find the general solution of the equation.

y'(t) = t²/(y² + 1); y(−1) = 1, y(0) = 0, y(−1) = −1

42–43. Implicit solutions for separable equations For the following separable equations, carry out the indicated analysis.

a. Find the general solution of the equation.

e⁻ʸᐟ²y'(x) = 4x sin x² − x; y(0) = 0, y(0) = ln(1/4), y(√(π/2)) = 0

brOrthogonal trajectories Two curves are orthogonal to each other if their tangent lines are perpendicular at each point of intersection. A family of curves forms orthogonal trajectories with another family of curves if each curve in one family is orthogonal to each curve in the other family. Use the following steps to find the orthogonal trajectories of the family of ellipses 2x² + y² = a²

b. The family of trajectories orthogonal to 2x² + y² = a² satisfies the differential equation dy/dx = y/(2x). Why?

Orthogonal trajectories Use the method in Exercise 44 to find the orthogonal trajectories for the family of circles x² + y² = a²

[Use of Tech] Analysis of a separable equation Consider the differential equation yy'(t) = ½eᵗ + t and carry out the following analysis.

a. Find the general solution of the equation and express it explicitly as a function of t in two cases: y > 0 and y < 0.

Blowup in finite time Consider the initial value problem y'(t) = yⁿ + 1, y(0) = y₀, where n is a positive integer.

b. Solve the initial value problem with n = 2 and y₀ = 1/√2.

{Use of Tech} Logistic equation for an epidemic When an infected person is introduced into a closed and otherwise healthy community, the number of people who contract the disease (in the absence of any intervention) may be modeled by the logistic equation

 dP/dt=kP(1−P/A),P0 =P_0, 

where K is a positive infection rate, A is the number of people in the community, and P0 is the number of infected people at t=0. The model also assumes no recovery. 

c. For a fixed value of K and A, describe the long-term behavior of the solutions, for any P0 with 0<P0<A. 

42–43. Implicit solutions for separable equations For the following separable equations, carry out the indicated analysis.

b. Find the value of the arbitrary constant associated with each initial condition. (Each initial condition requires a different constant.)

y'(t) = t²/(y² + 1); y(−1) = 1, y(0) = 0, y(−1) = −1

{Use of Tech} Logistic equation for spread of rumors Sociologists model the spread of rumors using logistic equations. The key assumption is that at any given time, a fraction y of the population, where 0≤y≤1, knows the rumor, while the remaining fraction 1−y does not. Furthermore, the rumor spreads by interactions between those who know the rumor and those who do not. The number of such interactions is proportional to y1−y. Therefore, the equation that describes the spread of the rumor is y′(t)=ky (1−y), for t≥0 where k is a positive real number and t is measured in weeks. The number of people who initially know the rumor is y(0)=y0, where 0≤y0≤1. 

a. Solve this initial value problem and give the solution in terms of k and y0.

{Use of Tech} Free fall An object in free fall may be modeled by assuming the only forces at work are the gravitational force and air resistance. By Newton’s Second Law of Motion (mass end . acceleration = the sum of external forces), the velocity of the object satisfies the differential equation 

m · v'(t) = mg + f(v)

mass | acceleration | external forces

where f is a function that models the air resistance (assuming the positive direction is downward). One common assumption (often used for motion in air) is that f(v)=−kv^2, for t≥0, where k>0 is a drag coefficient.

c. Find the solution of this separable equation assuming v(0)=0 and 0<v²<g/a.