{Use of Tech} Free fall Using th e background given in Exercise 47, assume the resistance is given by f(v)=−Rv, for t≥0, where R>0 is a drag coefficient (an assumption often made for a heavy medium such as water or oil).

c. Find the solution of this separable equation assuming v(0)=0 and 0<v<g/b .

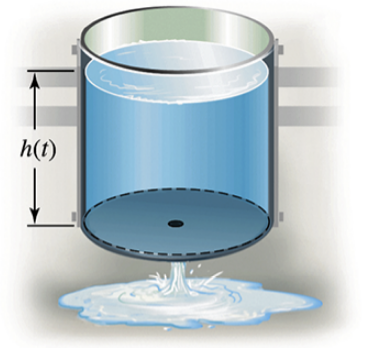
{Use of Tech} Torricelli’s law An open cylindrical tank initially filled with water drains through a hole in the bottom of the tank according to Torricelli’s law (see figure). If h(t) is the depth of water in the tank for t≥0 s, then Torricelli’s law implies h′(t)=−k√h, where k is a constant that includes g=9.8m/s², the radius of the tank, and the radius of the drain. Assume the initial depth of the water is h(0)=Hm. 

a. Find the solution of the initial value problem.

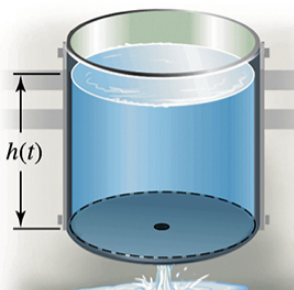
{Use of Tech} Torricelli’s law An open cylindrical tank initially filled with water drains through a hole in the bottom of the tank according to Torricelli’s law (see figure). If h(t) is the depth of water in the tank for t≥0 s, then Torricelli’s law implies h′(t)=−k√h, where k is a constant that includes g=9.8m/s², the radius of the tank, and the radius of the drain. Assume the initial depth of the water is h(0)=Hm. 

b. Find the solution in k=0.1the case that and H=0 .5m. 

{Use of Tech} Chemical rate equations Let y(t) be t he concentration of a substance in a chemical reaction (typical units are moles/liter). The change in the concentration, under appropriate conditions, is modeled by the equation dy/dt=-ky^n for t≥0, where k>0 is a rate constant and the positive integer n is the order of the reaction.

b. Solve the initial value problem for a second-order reaction (n=2) assuming y(0)=y0.

{Use of Tech} Tumor growth The Gompertz growth equation is often used to model the growth of tumors. Let M(t) be the mass of a tumor at time t≥0. The relevant initial value problem is 

dM/dt=−rM ln (M/K), M(0)=M0, 

where r and K are positive constants and 0<M0<K.

b. Solve the initial value problem and graph the solution for r=1, K=4, and M0=1. Describe the growth pattern of the tumor. Is the growth unbounded? If not, what is the limiting size of the tumor? 

[Use of Tech] Analysis of a separable equation Consider the differential equation yy'(t) = ½eᵗ + t and carry out the following analysis.

c. Graph the solutions in part (b) and describe their behavior as t increases. 

Cooling time Suppose an object with an initial temperature of T₀ > 0 is put in surroundings with an ambient temperature of A, where A < T₀/2. Let t₁/₂ be the time required for the object to cool to T₀/2.

c. Why is the condition A < T₀/2 needed?

Cooling time Suppose an object with an initial temperature of T₀ > 0 is put in surroundings with an ambient temperature of A, where A < T₀/2. Let t₁/₂ be the time required for the object to cool to T₀/2.

a. Show that t₁/₂ = −1/k ln((T₀ − 2A)/(2(T₀ − A))).

A bad loan Consider a loan repayment plan described by the initial value problem

B'(t)=0.03B−600,B(0)=40,000,

where the amount borrowed is B(0)=$40,000, the monthly payments are $600, and B(t) is the unpaid balance in the loan.

b. What is the most that you can borrow under the terms of this loan without going further into debt each month?

Case 2 of the general solution Solve the equation y′(t) = ky + b in the case that ky + b < 0 and verify that the general solution is y(t) = Ceᵏᵗ − b/k.

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample

b. If k>0 and b>0 then y(t)=0 is never a solution of y'(t)=ky−b.

{Use of Tech} Endowment model An endowment is an investment account in which the balance ideally remains constant and withdrawals are made on the interest earned by the account. Such an account may be modeled by the initial value problem B′(t)=rB−m, for t≥0, with B(0)=B0. The constant r>0 reflects the annual interest rate, m>0 is the annual rate of withdrawal, B0 is the initial balance in the account, and t is measured in years.

a. Solve the initial value problem with r=0.05,  m=$1000/year, and B0=$15,000 Does the balance in the account increase or decrease?

{Use of Tech} Intravenous drug dosing The amount of drug in the blood of a patient (in milligrams) administered via an intravenous line is governed by the initial value problem y’(t) = -0.02y + 3, y(0) = 0 where t is measured in hours.

b. What is the steady-state level of the drug?

{Use of Tech} Fish harvesting A fish hatchery has 500 fish at t=0, when harvesting begins at a rate of b>0 fish/year The fish population is modeled by the initial value problem y′(t)=0.01y−b, y(0)=500 where t is measured in years.

c. Graph the solution in the case that b=60 fish/year. Describe the solution.

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample

d. According to Newton’s Law of Cooling, the temperature of a hot object will reach the ambient temperature after a finite amount of time.

5–10. First-order linear equations Find the general solution of the following equations.

y'(x) = −y + 2

5–10. First-order linear equations Find the general solution of the following equations.

v'(y) − v/2 = 14

11–16. Initial value problems Solve the following initial value problems.

y'(x) = −y + 2, y(0) = −2

11–16. Initial value problems Solve the following initial value problems.

y'(t) − 3y = 12, y(1) = 4

23–26. Loan problems The following initial value problems model the payoff of a loan. In each case, solve the initial value problem, for t≥0 graph the solution, and determine the first month in which the loan balance is zero.

B′(t) = 0.005B − 500, B(0) = 50,000

27–30. Newton’s Law of Cooling Solve the differential equation for Newton’s Law of Cooling to find the temperature function in the following cases. Then answer any additional questions.

An iron rod is removed from a blacksmith’s forge at a temperature of 900°C . Assume k=0.02 and the rod cools in a room with a temperature of 30°C When does the temperature of the rod reach 100°C? 

Solving Bernoulli equations Use the method outlined in Exercise 43 to solve the following Bernoulli equations.

a. y′(t) + y = 2y²

23–26. Loan problems The following initial value problems model the payoff of a loan. In each case, solve the initial value problem, for t≥0 graph the solution, and determine the first month in which the loan balance is zero.

B′(t) = 0.004B − 800, B(0) = 40,000

27–30. Newton’s Law of Cooling Solve the differential equation for Newton’s Law of Cooling to find the temperature function in the following cases. Then answer any additional questions.

A pot of boiling soup (100°C) is put in a cellar with a temperature of 10°C. After 30 minutes, the soup has cooled to 80°C. When will the temperature of the soup reach 30°C 

What is the equilibrium solution of the equation y'(t) = 3y − 9? Is it stable or unstable?

The general solution of a first-order linear differential equation is y(t) = Ce⁻¹⁰ᵗ − 13. What solution satisfies the initial condition y(0) = 4?

39–42. Special equations A special class of first-order linear equations have the form a(t)y'(t)+a'(t)y(t)=f(t), where a and f are given functions of t. Notice that the left side of this equation can be written as the derivative of a product, so the equation has the form

a(t)y'(t) + a'(t)y(t) = d/dt (a(t)y(t)) = f(t). 

Therefore, the equation can be solved by integrating both sides with respect to t. Use this idea to solve the following initial value problems. 

t³y′(t) + 3t²y = (1 + t)/t, y(1) = 6

39–42. Special equations A special class of first-order linear equations have the form a(t)y'(t)+a'(t)y(t)=f(t), where a and f are given functions of t. Notice that the left side of this equation can be written as the derivative of a product, so the equation has the form

a(t)y'(t) + a'(t)y(t) = d/dt (a(t)y(t)) = f(t). 

Therefore, the equation can be solved by integrating both sides with respect to t. Use this idea to solve the following initial value problems. 

(t² + 1)y′(t) + 2ty = 3t², y(2) = 8

Solving Bernoulli equations Use the method outlined in Exercise 43 to solve the following Bernoulli equations.

c. y′(t) + y = √y

45–48. General first-order linear equations Consider the general first-order linear equation y'(t)+a(t)y(t)=f(t). This equation can be solved, in principle, by defining the integrating factor p(t)=exp (∫a(t)dt). Here is how the integrating factor works. Multiply both sides of the equation by p (which is always positive) and show that the left side becomes an exact derivative. Therefore, the equation becomes

p(t)(y′(t) + a(t)y(t)) = d/dt(p(t)y(t)) = p(t)f(t).

Now integrate both sides of the equation with respect to t to obtain the solution. Use this method to solve the following initial value problems. Begin by computing the required integrating factor.

y′(t) + (2t)/(t² + 1)y(t) = 1 + 3t², y(1) = 4