Back
BackProblem 12.4.33
31–38. Equations of parabolas Find an equation of the following parabolas. Unless otherwise specified, assume the vertex is at the origin.
A parabola with focus at (3, 0)
Problem 12.4.35
31–38. Equations of parabolas Find an equation of the following parabolas. Unless otherwise specified, assume the vertex is at the origin.
A parabola symmetric about the y-axis that passes through the point (2, -6)
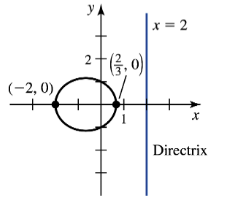
Problem 12.4.12
How does the eccentricity determine the type of conic section?
Problem 12.4.13
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
x² = 12y
Problem 12.4.45
39–50. Equations of ellipses and hyperbolas Find an equation of the following ellipses and hyperbolas, assuming the center is at the origin.
A hyperbola with vertices (±2, 0) and asymptotes y = ±3x/2
Problem 12.4.41
39–50. Equations of ellipses and hyperbolas Find an equation of the following ellipses and hyperbolas, assuming the center is at the origin.
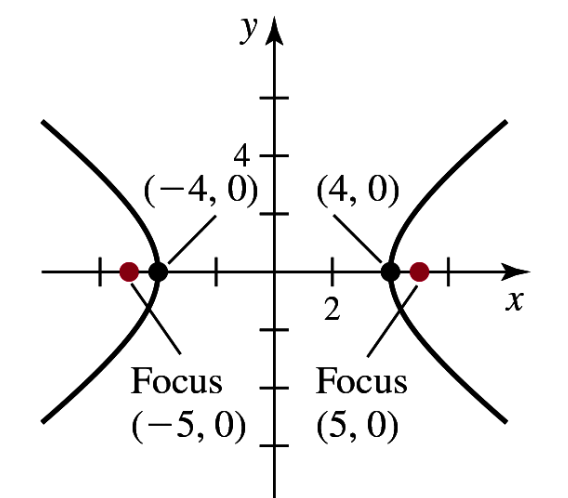
A hyperbola with vertices (±4, 0) and foci (±6, 0)
Problem 12.4.49
39–50. Equations of ellipses and hyperbolas Find an equation of the following ellipses and hyperbolas, assuming the center is at the origin.
Problem 12.4.43
39–50. Equations of ellipses and hyperbolas Find an equation of the following ellipses and hyperbolas, assuming the center is at the origin.
An ellipse with vertices (±5, 0), passing through the point (4, 3/5)
Problem 12.4.50
39–50. Equations of ellipses and hyperbolas Find an equation of the following ellipses and hyperbolas, assuming the center is at the origin.
Problem 12.4.51b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
b. On every ellipse, there are exactly two points at which the curve has slope s, where s is any real number.
Problem 12.4.51d
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
d. The point on a parabola closest to the focus is the vertex.
Problem 12.4.16
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
x²/9 + y²/4 = 1
Problem 12.4.69
69–72. Tangent lines Find an equation of the line tangent to the following curves at the given point.
x² = -6y; (-6, -6)
Problem 12.4.71
69–72. Tangent lines Find an equation of the line tangent to the following curves at the given point.
y² - x²/64 = 1; (6, -5/4)
Problem 12.4.92
90–94. Focal chords A focal chord of a conic section is a line through a focus joining two points of the curve. The latus rectum is the focal chord perpendicular to the major axis of the conic. Prove the following properties.
The length of the latus rectum of the parabola y ² =4px or x ² =4py is 4|p|.
Problem 12.4.74
Tangent lines for a hyperbola Find an equation of the line tangent to the hyperbola x²/a² + y²/b² = 1 at the point (x₀, y₀)
Problem 12.4.18
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
4x = -y²
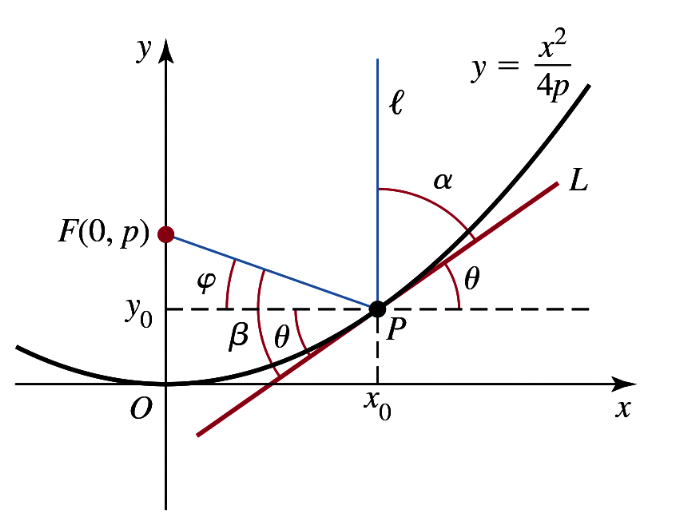
Problem 12.4.83a
Reflection property of parabolas: Consider the parabola y = x²/(4p) with its focus at F(0, p). The goal is to show that the angle of incidence (α) equals the angle of reflection (β).
a. Let P(x₀, y₀) be a point on the parabola. Show that the slope of the tangent line at P is tan θ = x₀/(2p).
Problem 12.4.21
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
4x² - y² = 16
Problem 12.4.22
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
25y² - 4x² = 100
Problem 12.4.26
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
x² + y²/9 = 1
Problem 12.4.30
13–30. Graphing conic sections Determine whether the following equations describe a parabola, an ellipse, or a hyperbola, and then sketch a graph of the curve. For each parabola, specify the location of the focus and the equation of the directrix; for each ellipse, label the coordinates of the vertices and foci, and find the lengths of the major and minor axes; for each hyperbola, label the coordinates of the vertices and foci, and find the equations of the asymptotes.
10x² - 7y² = 140
Problem 12.4.52
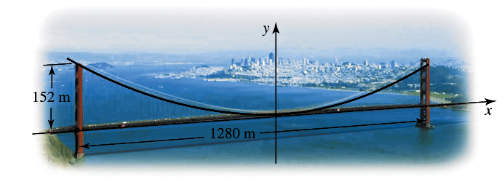
Golden Gate Bridge Completed in 1937, San Francisco’s Golden Gate Bridge is 2.7 km long and weighs about 890,000 tons. The length of the span between the two central towers is 1280 m; the towers themselves extend 152 m above the roadway. The cables that support the deck of the bridge between the two towers hang in a parabola (see figure). Assuming the origin is midway between the towers on the deck of the bridge, find an equation that describes the cables. How long is a guy wire that hangs vertically from the cables to the roadway 500 m from the center of the bridge?
Problem 12.4.54
53–56. Eccentricity-directrix approach Find an equation of the following curves, assuming the center is at the origin. Sketch a graph labeling the vertices, foci, asymptotes (if they exist), and directrices. Use a graphing utility to check your work.
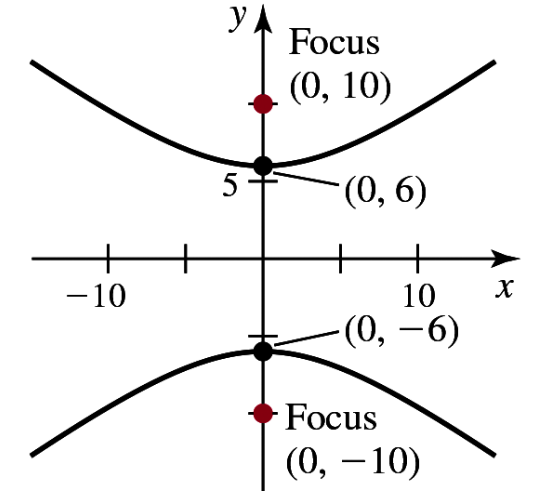
An ellipse with vertices (0, ±9) and eccentricity ¼
Problem 12.4.58
57–62. Polar equations for conic sections Graph the following conic sections, labeling the vertices, foci, directrices, and asymptotes (if they exist). Use a graphing utility to check your work.
r = 3/(2 + cos θ)
Problem 12.4.61
57–62. Polar equations for conic sections Graph the following conic sections, labeling the vertices, foci, directrices, and asymptotes (if they exist). Use a graphing utility to check your work.
r = 1/(2 - 2 sin θ)
Problem 12.4.65
63–66. Tracing hyperbolas and parabolas Graph the following equations. Then use arrows and labeled points to indicate how the curve is generated as θ increases from 0 to 2π.
r = 3/(1 - cos θ)
Problem 12.4.76
75–76. Graphs to polar equations Find a polar equation for each conic section. Assume one focus is at the origin.
Problem 12.4.78a
The ellipse and the parabola: Let R be the region bounded by the upper half of the ellipse x²/2 + y² = 1 and the parabola y = x²/√2
a. Find the area of R
Problem 12.4.80a
Area of a sector of a hyperbola: Consider the region R bounded by the right branch of the hyperbola x²/a² - y²/b² = 1 and the vertical line through the right focus
a. What is the area of R?