Back
BackProblem 12.3.39
33–40. Areas of regions Make a sketch of the region and its bounding curves. Find the area of the region.
The region inside one leaf of r = cos 3θ
Problem 12.3.41
41–44. Intersection points and area Find all the intersection points of the following curves. Find the area of the entire region that lies within both curves
r = 3 sin θ and r = 3 cos θ
Problem 12.3.43
41–44. Intersection points and area Find all the intersection points of the following curves. Find the area of the entire region that lies within both curves
r = 1 + sin θ and r = 1 + cos θ
Problem 12.3.45
45–60. Areas of regions Find the area of the following regions.
The region outside the circle r = 1/2 and inside the circle r = cos θ
Problem 12.3.47
45–60. Areas of regions Find the area of the following regions.
The region inside the curve r = √(cos θ) and inside the circle r = 1/√2 in the first quadrant
Problem 12.3.49
45–60. Areas of regions Find the area of the following regions.
The region inside one leaf of the rose r = cos 5θ
Problem 12.3.51
45–60. Areas of regions Find the area of the following regions.
The region inside the rose r = 4 sin 2θ and inside the circle r = 2
Problem 12.3.53
45–60. Areas of regions Find the area of the following regions.
The region common to the circles r = 2 sin θ and r = 1
Problem 12.3.55
45–60. Areas of regions Find the area of the following regions.
The region inside the outer loop but outside the inner loop of the limaçon r = 3 - 6 sin θ
Problem 12.3.57
45–60. Areas of regions Find the area of the following regions.
The region inside the lemniscate r² = 6 sin 2θ
Problem 12.3.59
45–60. Areas of regions Find the area of the following regions.
The region inside the limaçon r = 4 - 2 cos θ
Problem 12.3.63
63–74. Arc length of polar curves Find the length of the following polar curves.
The complete circle r = a sin θ, where a > 0
Problem 12.3.65
63–74. Arc length of polar curves Find the length of the following polar curves.
The spiral r = θ², for 0 ≤ θ ≤ 2π
Problem 12.3.67
63–74. Arc length of polar curves Find the length of the following polar curves.
The complete cardioid r = 4 + 4 sin θ
Problem 12.3.73
63–74. Arc length of polar curves Find the length of the following polar curves.
{Use of Tech} The complete limaçon r=4−2cosθ
Problem 12.3.76
63–74. Arc length of polar curves Find the length of the following polar curves.
{Use of Tech} The complete limaçon r=4−2cosθ
Problem 12.3.78
Spiral arc length Consider the spiral r=4θ, for θ≥0.
a. Use a trigonometric substitution to find the length of the spiral, for 0≤θ≤√8.
Problem 12.3.78c
Spiral arc length Consider the spiral r=4θ, for θ≥0.
c. Show that L′(θ)>0. Is L″(θ) positive or negative? Interpret your answer.
Problem 12.3.80a
Area of roses Assume m is a positive integer.
a. Even number of leaves: What is the relationship between the total area enclosed by the 4m-leaf rose r=cos(2mθ) and m?
Problem 12.3.81a
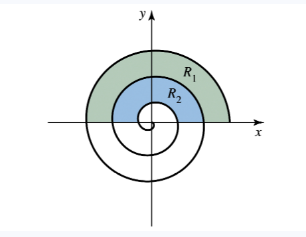
Regions bounded by a spiral: Let Rₙ be the region bounded by the nth turn and the (n+1)st turn of the spiral r = e⁻ᶿ in the first and second quadrants, for θ ≥ 0 (see figure).
a. Find the area Aₙ of Rₙ.
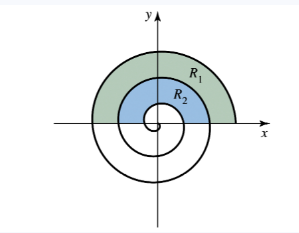
Problem 12.3.81c
Regions bounded by a spiral: Let Rₙ be the region bounded by the nth turn and the (n+1)st turn of the spiral r = e⁻ᶿ in the first and second quadrants, for θ ≥ 0 (see figure).
c. Evaluate lim(n→∞) Aₙ₊₁/Aₙ.
Problem 12.3.82b
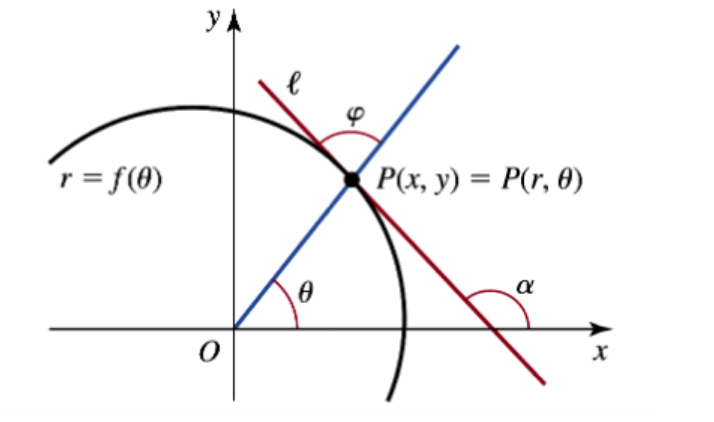
Tangents and normals: Let a polar curve be described by r = f(θ), and let ℓ be the line tangent to the curve at the point P(x,y) = P(r,θ) (see figure).
b. Explain why tan θ = y/x.
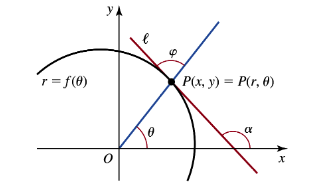
Problem 12.3.82e
Tangents and normals: Let a polar curve be described by r = f(θ), and let ℓ be the line tangent to the curve at the point P(x,y) = P(r,θ) (see figure).
e. Prove that the values of θ for which ℓ is parallel to the y-axis satisfy tan θ = f(θ)/f'(θ).
Problem 12.3.84
84. Arc length for polar curves: Prove that the length of the curve r = f(θ) for α ≤ θ ≤ β is
L = ∫(α to β) √(f(θ)² + f'(θ)²) dθ.
Problem 12.3.85
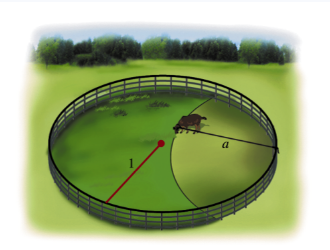
85–87. Grazing goat problems Consider the following sequence of problems related to grazing goats tied to a rope. (See the Guided Project Grazing goat problems.)
A circular corral of unit radius is enclosed by a fence. A goat inside the corral is tied to the fence with a rope of length 0≤a≤2 (see figure). What is the area of the region (inside the corral) that the goat can graze? Check your answer with the special cases a=0 and a=2.
Problem 12.3.1
Express the polar equation r=f(θ) in parametric form in Cartesian coordinates, where θ is the parameter.
Problem 12.3.2
Explain why the slope of the line θ=π/2 is undefined.
Problem 12.4.38
31–38. Equations of parabolas Find an equation of the following parabolas. Unless otherwise specified, assume the vertex is at the origin.
Problem 12.4.37
31–38. Equations of parabolas Find an equation of the following parabolas. Unless otherwise specified, assume the vertex is at the origin.
Problem 12.4.31
31–38. Equations of parabolas Find an equation of the following parabolas. Unless otherwise specified, assume the vertex is at the origin.
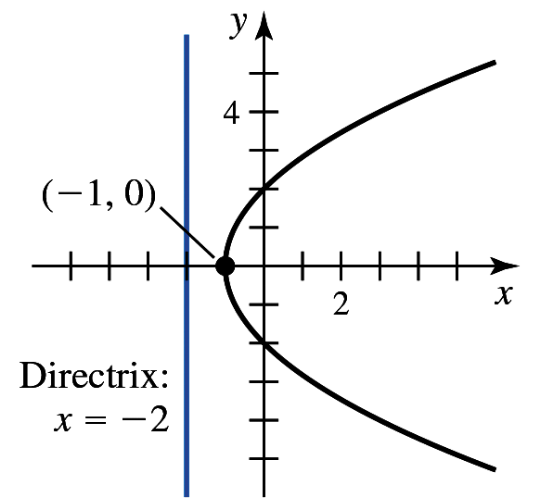
A parabola that opens to the right with directrix x = -4