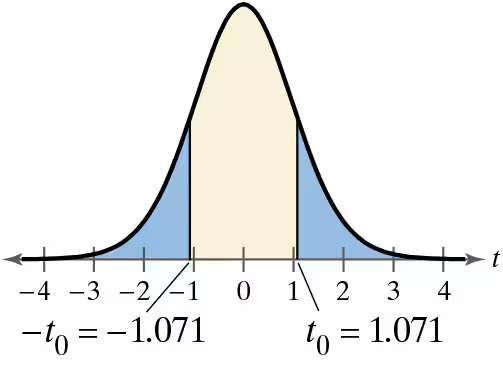
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
c. t = -2.096
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 5:12m
5:12mMaster Intro to Hypothesis Testing with a bite sized video explanation from Patrick
Start learning