Textbook Question
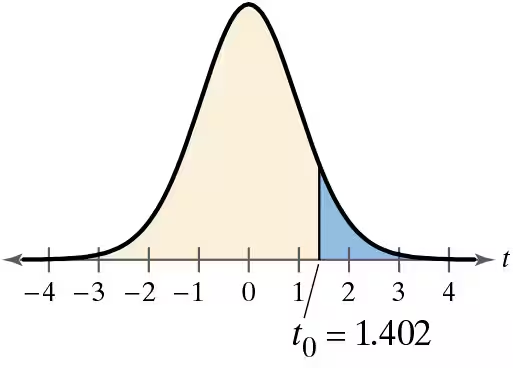
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Right-tailed test, α=0.05, n=23
17
views
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
1:47 minutesProblem 7.4.10a
Textbook Question
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
a. t = 1.4
Verified step by step guidance1
Step 1: Understand the context of the problem. The standardized test statistic t = 1.402 is given, and the goal is to determine whether this value allows you to reject the null hypothesis. This decision depends on the critical value of t and the significance level (α).
Step 2: Analyze the graph provided. The graph shows a t-distribution curve with the test statistic t₀ = 1.402 marked. The shaded region represents the area in the tail of the distribution, which corresponds to the p-value or the probability of observing a test statistic as extreme as t₀ under the null hypothesis.
Step 3: Compare the test statistic t₀ to the critical value. If the test statistic falls in the rejection region (typically in the tails of the distribution beyond the critical value), the null hypothesis can be rejected. The critical value depends on the degrees of freedom and the chosen significance level (α).
Step 4: Interpret the shaded region. If the area of the shaded region (p-value) is less than the significance level (α), it indicates strong evidence against the null hypothesis, and you can reject it. Otherwise, you fail to reject the null hypothesis.
Step 5: Conclude based on the comparison. If the test statistic t₀ = 1.402 does not exceed the critical value or the p-value is greater than α, you fail to reject the null hypothesis. If it does exceed the critical value or the p-value is less than α, you reject the null hypothesis.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Null Hypothesis
The null hypothesis is a statement that there is no effect or no difference, and it serves as the default assumption in hypothesis testing. Researchers aim to gather evidence against the null hypothesis to support an alternative hypothesis. In this context, rejecting the null hypothesis indicates that the observed data is statistically significant.
Recommended video:
Guided course
06:21
Step 1: Write Hypotheses
t-Distribution
The t-distribution is a type of probability distribution that is symmetric and bell-shaped, similar to the normal distribution but with heavier tails. It is used in hypothesis testing, particularly when sample sizes are small or when the population standard deviation is unknown. The shape of the t-distribution changes with the degrees of freedom, affecting the critical values for hypothesis testing.
Recommended video:
05:50Critical Values: t-Distribution
Critical Value and Rejection Region
The critical value is a threshold that determines the boundary for rejecting the null hypothesis in hypothesis testing. The rejection region is the area in the tails of the distribution where, if the test statistic falls, the null hypothesis can be rejected. In the provided graph, the shaded area indicates the rejection region, and the position of the test statistic t = 1.4 relative to this region is crucial for making a decision about the null hypothesis.
Recommended video:
05:50Critical Values: t-Distribution
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice