Back
BackProblem 8.2.16
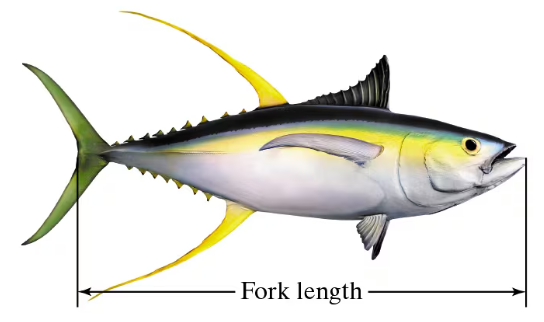
Yellowfin Tuna
A marine biologist claims that the mean fork length (see figure at the left) of yellowfin tuna is different in two zones in the eastern tropical Pacific Ocean. A sample of 26 yellowfin tuna collected in Zone A has a mean fork length of 76.2 centimeters and a standard deviation of 16.5 centimeters. A sample of 31 yellowfin tuna collected in Zone B has a mean fork length of 80.8 centimeters and a standard deviation of 23.4 centimeters. At ,α=0.01 can you support the marine biologist’s claim? Assume the population variances are equal. (Adapted from Fishery Bulletin)
Problem 8.2.25
Constructing Confidence Intervals for μ1-μ2. When the sampling distribution for x̅1-x̅2 is approximated by a t-distribution and the populations have equal variances, you can construct a confidence interval for μ1-μ2, as shown below.
Construct the indicated confidence interval for μ1-μ2 . Assume the populations are approximately normal with equal variances.
Family Doctor
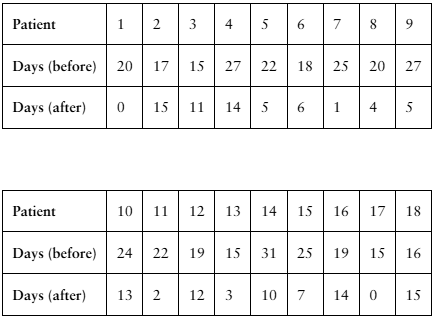
To compare the mean number of days spent waiting to see a family doctor for two large cities, you randomly select several people in each city who have had an appointment with a family doctor. The results are shown at the left. Construct a 90% confidence interval for the difference in mean number of days spent waiting to see a family doctor for the two cities. (Adapted from Merritt Hawkins)
Problem 8.2.26
Constructing Confidence Intervals for μ1-μ2. When the sampling distribution for x̅1-x̅2 is approximated by a t-distribution and the populations have equal variances, you can construct a confidence interval for μ1-μ2, as shown below.
Construct the indicated confidence interval for μ1-μ2 . Assume the populations are approximately normal with equal variances.
10K Race
To compare the mean ages of male and female participants in a 10K race, you randomly select several ages from both sexes. The results are shown below. Construct a 95% confidence interval for the difference in mean ages of male and female participants in the race. (Adapted from Great Race)
Problem 8.2.12
Test the claim about the difference between two population means and at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.
Claim: μ1>μ2, α=0.01, Assume (σ1)^2≠(σ2)^2
Sample statistics:
x̅1=52, s1=4.8, n1=32 and x̅2=50, s2=1.2, n2=40
Problem 8.2.14c
Testing the Difference Between Two Means, (c) find the standardized test statistic t,
Assume the samples are random and independent, and the populations are normally distributed.
Transactions
A magazine claims that the mean amount spent by a customer at Burger Stop is greater than the mean amount spent by a customer at Fry World. The results for samples of customer transactions for the two fast food restaurants are shown at the left. At , α=0.05 can you support the magazine’s claim? Assume the population variances are equal.
Problem 8.2.14d
Testing the Difference Between Two Means,
(d) decide whether to reject or fail to reject the null hypothesis. Assume the samples are random and independent, and the populations are normally distributed.
Transactions
A magazine claims that the mean amount spent by a customer at Burger Stop is greater than the mean amount spent by a customer at Fry World. The results for samples of customer transactions for the two fast food restaurants are shown at the left. At , α=0.05 can you support the magazine’s claim? Assume the population variances are equal.
Problem 8.2.14e
Testing the Difference Between Two Means, (e) interpret the decision in the context of the original claim.
Assume the samples are random and independent, and the populations are normally distributed.
Transactions
A magazine claims that the mean amount spent by a customer at Burger Stop is greater than the mean amount spent by a customer at Fry World. The results for samples of customer transactions for the two fast food restaurants are shown at the left. At , α=0.05 can you support the magazine’s claim? Assume the population variances are equal.
Problem 8.3.3
Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed.
Claim: μd<0 , α=0.05 , Sample statistics: d̄ =1.5 , sd=3.2 , n=14
Problem 8.3.1
What conditions are necessary to use the dependent samples t-test for the mean of the differences for a population of paired data?
Problem 8.3.5
Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed.
Claim: μd≤0 , α=0.10, Sample statistics: d̄ =6.5, sd=9.54, n=16
Problem 8.3.23
Constructing Confidence Intervals for μd To construct a confidence interval for μd , use the inequality below.
Construct the indicated confidence interval for μd . Assume the populations are normally distributed.
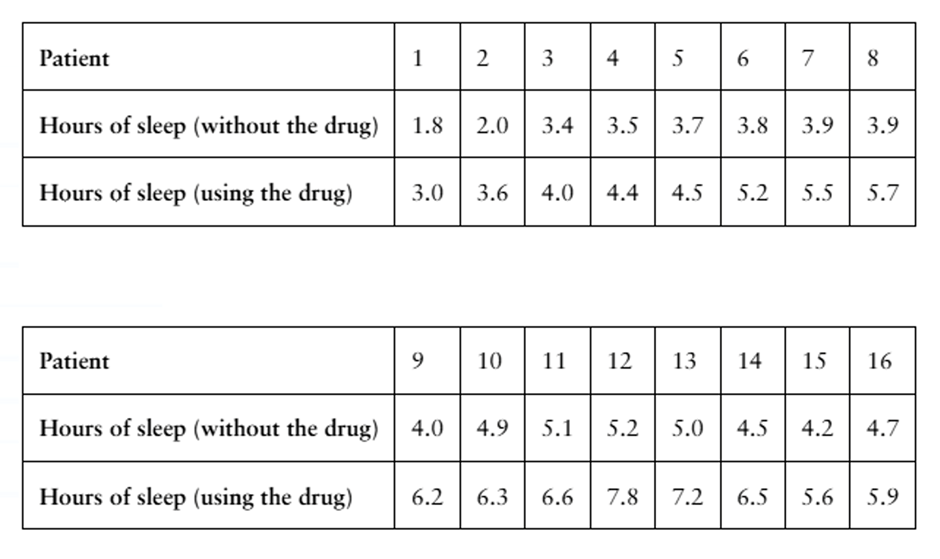
[APPLET] Drug Testing A sleep disorder specialist wants to test the effectiveness of a new drug that is reported to increase the number of hours of sleep patients get during the night. To do so, the specialist randomly selects 16 patients and records the number of hours of sleep each gets with and without the new drug. The table shows the results of the two-night study. Construct a 90% confidence interval for μd.
Problem 8.3.14
Testing the Difference Between Two Means (a) identify the claim and state Ho and Ha , (b) find the critical value(s) and identify the rejection region(s), (c) calculate d̄ and Sd, (d) find the standardized test statistic t, (e) decide whether to reject or fail to reject the null hypothesis, and (f ) interpret the decision in the context of the original claim. Assume the samples are random and dependent, and the populations are normally distributed.
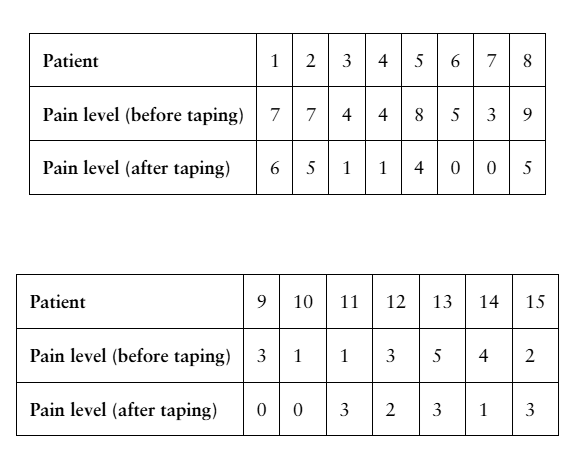
[APPLET] Therapeutic Taping
A physical therapist claims that the use of a specific type of therapeutic tape reduces pain in patients with chronic tennis elbow. The table shows the pain levels on a scale of 0 to 10, where 0 is no pain and 10 is the worst pain possible, for 15 patients with chronic tennis elbow when holding a 1 kilogram weight. At , α=0.05 is there enough evidence to support the therapist’s claim? (Adapted from BioMed Central, Ltd.)
Problem 8.3.9a
Testing the Difference Between Two Means (a) identify the claim and state Ho and Ha
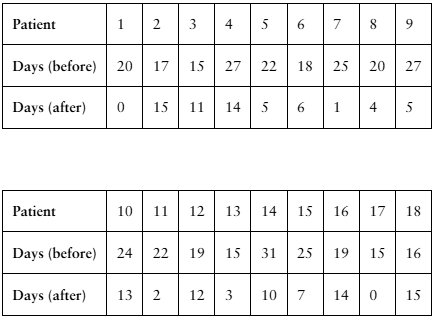
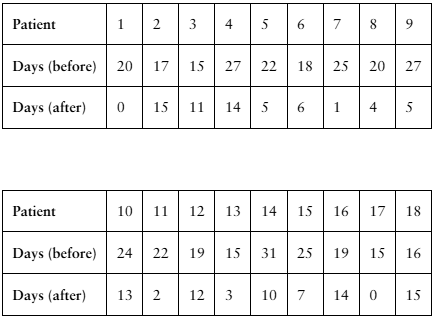
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.9b
Testing the Difference Between Two Means, (b) find the critical value(s) and identify the rejection region(s), Assume the samples are random and dependent, and the populations are normally distributed.
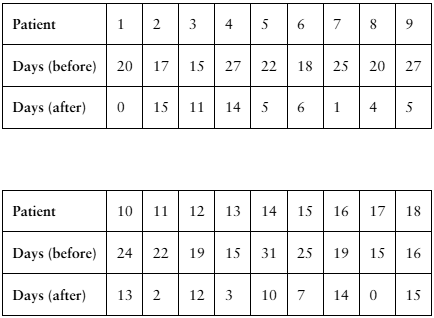
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.9c
Testing the Difference Between Two Means (c) calculate d̄ and Sd, Assume the samples are random and dependent, and the populations are normally distributed.
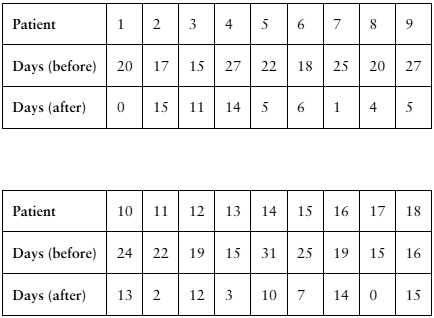
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.9d
Testing the Difference Between Two Means (d) find the standardized test statistic t, Assume the samples are random and dependent, and the populations are normally distributed.
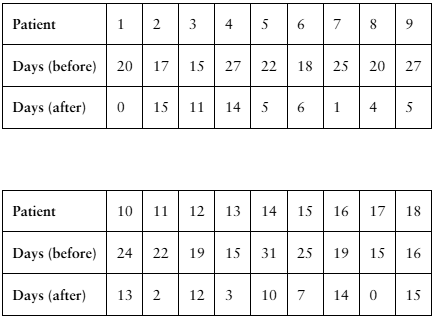
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.9e
Testing the Difference Between Two Means (e) decide whether to reject or fail to reject the null hypothesis, Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.9f
Testing the Difference Between Two Means (f ) interpret the decision in the context of the original claim. Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Migraines
A researcher claims that injections of onabotulinumtoxinA reduce the number of days per month that chronic migraine sufferers have headaches. The table shows the number of days chronic migraine sufferers suffered migraines before and after using the treatment. At , α= 0.01 is there enough evidence to support the researcher’s claim? (Adapted from Journal of Headache and Pain)
Problem 8.3.12a
Testing the Difference Between Two Means (a) identify the claim and state Ho and Ha ,Assume the samples are random and dependent, and the populations are normally distributed.
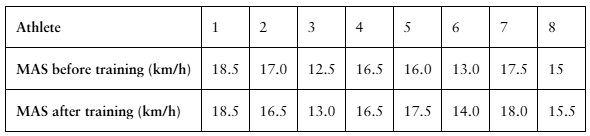
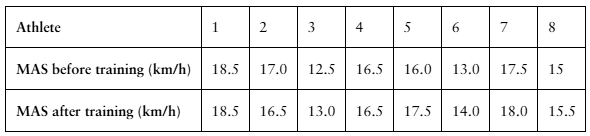
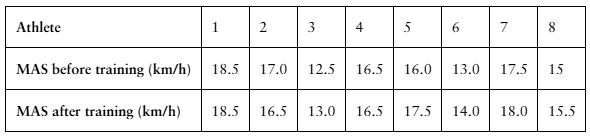
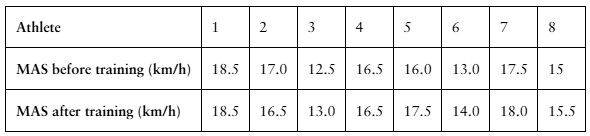
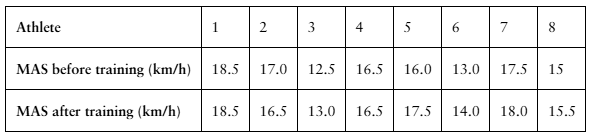
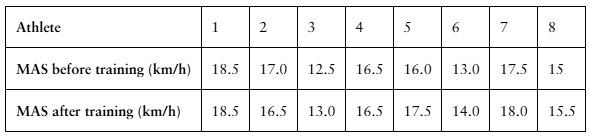
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.12b
Testing the Difference Between Two Means (b) find the critical value(s) and identify the rejection region(s), Assume the samples are random and dependent, and the populations are normally distributed.
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.12c
Testing the Difference Between Two Means (c) calculate d̄ and Sd, Assume the samples are random and dependent, and the populations are normally distributed.
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.12d
Testing the Difference Between Two Means (d) find the standardized test statistic t, Assume the samples are random and dependent, and the populations are normally distributed.
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.12e
Testing the Difference Between Two Means (e) decide whether to reject or fail to reject the null hypothesis, Assume the samples are random and dependent, and the populations are normally distributed.
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.12f
Testing the Difference Between Two Means (f ) interpret the decision in the context of the original claim. Assume the samples are random and dependent, and the populations are normally distributed.
Interval Training
A researcher claims that sprint interval training improves running performance in trained athletes. The table shows the maximum aerobic speed (MAS), in kilometers per hour, of trained athletes before and after six sessions of sprint interval training. At , α=0.10 is there enough evidence to support the researcher’s claim? (Adapted from National Strength and Conditioning Association)
Problem 8.3.8
Test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed.
Claim: μd≠0 , α=0.10, Sample statistics: d̄ =-1, sd=2.75, n=20
Problem 8.3.18a
Testing the Difference Between Two Means (a) identify the claim and state Ho and Ha .Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Passing Play Percentages The passing play percentages of 10 randomly selected NCAA Division 1A college football teams for home and away games in the 2020–2021 season are shown in the table. At , α=0.20 is there enough evidence to support the claim that passing play percentage is different for home and away games? (Source: TeamRankings)
Problem 8.3.18b
Testing the Difference Between Two Means (b) find the critical value(s) and identify the rejection region(s), Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Passing Play Percentages The passing play percentages of 10 randomly selected NCAA Division 1A college football teams for home and away games in the 2020–2021 season are shown in the table. At , α=0.20 is there enough evidence to support the claim that passing play percentage is different for home and away games? (Source: TeamRankings)
Problem 8.3.18c
Testing the Difference Between Two Means (c) calculate d̄ and Sd, Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Passing Play Percentages The passing play percentages of 10 randomly selected NCAA Division 1A college football teams for home and away games in the 2020–2021 season are shown in the table. At , α=0.20 is there enough evidence to support the claim that passing play percentage is different for home and away games? (Source: TeamRankings)
Problem 8.3.18d
Testing the Difference Between Two Means (d) find the standardized test statistic t, Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Passing Play Percentages The passing play percentages of 10 randomly selected NCAA Division 1A college football teams for home and away games in the 2020–2021 season are shown in the table. At , α=0.20 is there enough evidence to support the claim that passing play percentage is different for home and away games? (Source: TeamRankings)
Problem 8.3.18e
Testing the Difference Between Two Means (e) decide whether to reject or fail to reject the null hypothesis. Assume the samples are random and dependent, and the populations are normally distributed.
[APPLET] Passing Play Percentages The passing play percentages of 10 randomly selected NCAA Division 1A college football teams for home and away games in the 2020–2021 season are shown in the table. At , α=0.20 is there enough evidence to support the claim that passing play percentage is different for home and away games? (Source: TeamRankings)