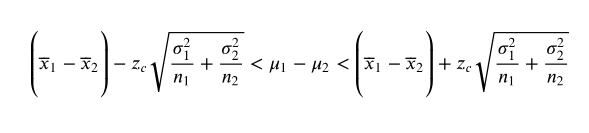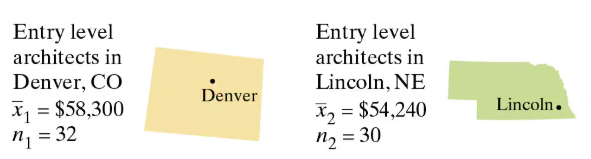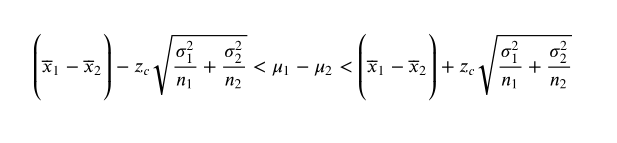Constructing Confidence Intervals for μ1-μ2. You can construct a confidence interval for the difference between two population means μ1-μ2 , as shown below, when both population standard deviations are known, and either both populations are normally distributed or both n1>= 30 and n2>=30 . Also, the samples must be randomly selected and independent.

[Image]

In Exercises 29 and 30, construct the indicated confidence interval for μ1-μ2 .

Software Engineer Salaries Construct a 95% confidence interval for the difference between the mean annual salaries of entry level software engineers in Santa Clara, California, and Greenwich, CT, using the data from Exercise 27.

Independent and Dependent Samples In Exercises 5– 8, classify the two samples as independent or dependent and justify your answer.

Sample 1: The IQ scores of 60 females

Sample 2: The IQ scores of 60 males

In Exercises 7–10, the statement represents a claim. Write its complement and state which is Ho and which is Ha.

μ≠2.28

In Exercises 11 –14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1=μ2; α=0.1

Population statistics:σ1=3.4 and σ2=1.5

Sample Statistics: x̅1=16, n1=29, x̅2=14, n2=28

In Exercises 11 –14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1>μ2; α=0.10

Population statistics:σ1=40 and σ2=15

Sample Statistics: x̅1=500, n1=100, x̅2=495, n2=75

Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Bed-in-a-Box To compare customer satisfaction with mattresses that are delivered compressed in a box and traditional mattresses, a researcher randomly selects 30 ratings of mattresses in boxes and 30 ratings of traditional mattresses. The mean rating of mattresses in boxes is 68.7 out of 100. Assume the population standard deviation is 6.6. The mean rating of traditional mattresses is 70.9 out of 100. Assume the population standard deviation is 5.6. At α=0.01, can the researcher support the claim that the mean rating of traditional mattresses is greater than the mean rating of mattresses in a box? (Adapted from Consumer Reports)

Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Repair Costs: Washing Machines You want to buy a washing machine, and a salesperson tells you that the mean repair costs for Model A and Model B are equal. You research the repair costs. The mean repair cost of 24 Model A washing machines is $208. Assume the population standard deviation is $18. The mean repair cost of 26 Model B washing machines is $221. Assume the population standard deviation is $22. At α=0.01, can you reject the salesperson’s claim?

Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Home Prices A real estate agency says that the mean home sales price in Casper, Wyoming, is the same as in Cheyenne, Wyoming. The mean home sales price for 35 homes in Casper is $349,237. Assume the population standard deviation is $158,005. The mean home sales price for 41 homes in Cheyenne is $435,244. Assume the population standard deviation is $154,716. At α=0.01, is there enough evidence to reject the agency’s claim? (Adapted from Realtor.com)

"Testing the Difference Between Two Means In Exercises 15–24, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

[APPLET] Precipitation A climatologist claims that the precipitation in Seattle, Washington, was greater than in Birmingham, Alabama, in a recent year. The daily precipitation amounts (in inches) for 30 days in a recent year in Seattle are shown below. Assume the population standard deviation is 0.25 inch.

0.00 0.00 0.05 0.01 0.21 0.00 0.00 0.52 0.00 0.010.00 0.19 0.00 0.18 0.02 0.02 0.13 0.00 0.03 0.000.04 0.00 0.41 0.23 0.00 0.80 0.15 0.00 0.00 0.79

The daily precipitation amounts (in inches) for 30 days in a recent year in Birmingham are shown below. Assume the population standard deviation is 0.52 inch.

0.00 0.96 0.84 0.00 0.10 0.00 0.00 0.20 0.00 0.54 0.97 0.00 0.35 0.02 0.04 0.70 0.00 0.00 0.00 0.00 0.03 0.01 0.15 0.27 0.00 0.00 0.93 0.00 0.89 0.01

At α=0.05, can you support the climatologist’s claim? (Source: NOAA)"

Constructing Confidence Intervals for μ1-μ2. You can construct a confidence interval for the difference between two population means μ1-μ2 , as shown below, when both population standard deviations are known, and either both populations are normally distributed or both n1>= 30 and n2>=30 . Also, the samples must be randomly selected and independent.

In Exercises 29 and 30, construct the indicated confidence interval for μ1-μ2 .

Architect Salaries Construct a 99% confidence interval for the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Lincoln, Nebraska, using the data from Exercise 28.

Testing a Difference Other Than Zero Sometimes a researcher is interested in testing a difference in means other than zero. In Exercises 27 and 28, you will test the difference between two means using a null hypothesis of Ho: μ1-μ2=k, Ho: μ1-μ2>=k or Ho: μ1-μ2<=k . The standardized test statistic is still

Architect Salaries Is the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Lincoln, Nebraska, equal to $9000? To decide, you select a random sample of entry level architects from each city. The results of each survey are shown in the figure. Assume the population standard deviations are σ1=$6560 and σ2=$6100 . At α=0.01 what should you conclude? (Adapted from Salary.com)

What conditions are necessary in order to use the z-test to test the difference between two population means?

The mean room rate for two adults for a random sample of 26 three-star hotels in Cincinnati has a sample standard deviation of $31. Assume the population is normally distributed. (Adapted from Expedia)

Construct a 99% confidence interval for the population standard deviation.

Testing the Difference Between Two Means, (a) identify the claim and state H0 and Ha , (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic t, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Pet Food

A pet association claims that the mean annual costs of food for dogs and cats are the same. The results for samples of the two types of pets are shown at the left. At , α=0.10 can you reject the pet association’s claim? Assume the population variances are equal. (Adapted from American Pet Products Association)

What conditions are necessary to use the t-test for testing the difference between two population means?

Explain how to perform a two-sample t-test for the difference between two population means.

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal and (b) not equal.

Ha:μ1>μ2 , α=0.01 , n1=12 , n2=15

[APPLET] Teaching Methods

A new method of teaching reading is being tested on third grade students. A group of third grade students is taught using the new curriculum. A control group of third grade students is taught using the old curriculum. The reading test scores for the two groups are shown in the back-to-back stem-and-leaf plot.

At , α=0.10 is there enough evidence to support the claim that the new method of teaching reading produces higher reading test scores than the old method does? Assume the population variances are equal.

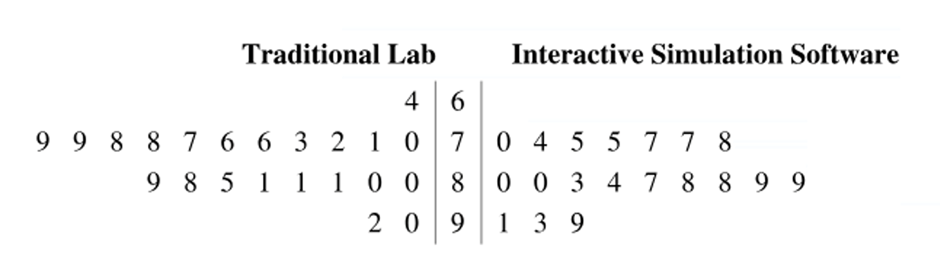
[APPLET] Teaching Methods

Two teaching methods and their effects on science test scores are being reviewed. A group of students is taught in traditional lab sessions. A second group of students is taught using interactive simulation software. The science test scores for the two groups are shown in the back-to-back stem-and-leaf plot.

At , α=0.01 can you support the claim that the mean science test score is lower for students taught using the traditional lab method than it is for students taught using the interactive simulation software? Assume the population variances are equal.

Constructing Confidence Intervals for μ1-μ2, When the sampling distribution for x̅1-x̅2 is approximated by a t-distribution and the population variances are not equal, you can construct a confidence interval for μ1-μ2 , as shown below.

construct the indicated confidence interval for μ1-μ2 . Assume the populations are approximately normal with unequal variances.

10K Race

To compare the mean finishing times of male and female participants in a 10K race, you randomly select several finishing times from both sexes. The results are shown at the left. Construct an 80% confidence interval for the difference in mean finishing times of male and female participants in the race. (Adapted from Great Race)

Blue Crabs A marine researcher claims that the stomachs of blue crabs from one location contain more fish than the stomachs of blue crabs from another location. The stomach contents of a sample of 25 blue crabs from Location A contain a mean of 320 milligrams of fish and a standard deviation of 60 milligrams. The stomach contents of a sample of 15 blue crabs from Location B contain a mean of 280 milligrams of fish and a standard deviation of 80 milligrams. At , α= 0.01can you support the marine researcher’s claim? Assume the population variances are equal.

Annual Income

A politician claims that the mean household income in a recent year is greater in York County, South Carolina, than it is in Elmore County, Alabama. In York County, a sample of 23 residents has a mean household income of $64,900 and a standard deviation of $16,000. In Elmore County, a sample of 19 residents has a mean household income of $59,500 and a standard deviation of $23,600. At , α= 0.05can you support the politician’s claim? Assume the population variances are not equal. (Adapted from U.S. Census Bureau)

[APPLET] Tensile Strength

The tensile strength of a metal is a measure of its ability to resist tearing when it is pulled lengthwise. An experimental method of treatment produced steel bars with the tensile strengths (in newtons per square millimeter) listed below.

Experimental Method:

391 383 333 378 368 401 339 376 366 348

The conventional method produced steel bars with the tensile strengths (in newtons per square millimeter) listed below.

Conventional Method:

362 382 368 398 381 391 400410 396 411 385 385 395 371

At , α=0.01 can you support the claim that the experimental method of treatment makes a difference in the tensile strength of steel bars? Assume the population variances are equal.

Test the claim about the difference between two population means and at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1≤μ2, α=0.05, Assume (σ1)^2≠(σ2)^2

Sample statistics:

x̅1=2410, s1=175, n1=13 and x̅2=2305, s2=52, n2=10

Test the claim about the difference between two population means and at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1=μ2, α=0.01, Assume (σ1)^2=(σ2)^2

Sample statistics:

x̅1=33.7, s1=3.5 , n1=12 and x̅2=35.5 , s2=2.2 , n2=17

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal

Ha:μ1≠μ2 , α=0.10 , n1=11 , n2=14

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal

Ha:μ1<μ2 , α=0.05 , n1=7 , n2=11

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal

Ha:μ1≠μ2 , α=0.01 , n1=19 , n2=22

Find the critical value(s) for the alternative hypothesis, level of significance , and sample sizes and . Assume that the samples are random and independent, the populations are normally distributed, and the population variances are (a) equal .

Ha:μ1<μ2 , α=0.10 , n1=30 , n2=32

Test the claim about the difference between two population means and at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1<μ2, α=0.10, Assume (σ1)^2=(σ2)^2

Sample statistics:

x̅1=0.345, s1=0.305 , n1=11 and x̅2=0.515, s2=0.215, n2=9