Back
BackProblem 6.6.19
Find the area of the surface generated when the given curve is revolved about the given axis.
x=√12y−y^2, for 2≤y≤10; about the y-axis
Problem 6.6.1
What is the area of the curved surface of a right circular cone of radius 3 and height 4?
Problem 6.6.3
Assume f is a nonnegative function with a continuous first derivative on [a, b]. The curve y=f(x) on [a, b] is revolved about the x-axis. Explain how to find the area of the surface that is generated.
Problem 6.6.5a
A surface is generated by revolving the line f(x)=2−x, for 0≤x≤2, about the x-axis. Find the area of the resulting surface in the following ways.
a. Using calculus
Problem 6.6.21
A 1.5-mm layer of paint is applied to one side of the following surfaces. Find the approximate volume of paint needed. Assume x and y are measured in meters.
The spherical zone generated when the curve y=√8x−x^2 on the interval 1≤x≤7 is revolved about the x-axis
Problem 6.6.23a
Determine whether the following statements are true and give an explanation or counterexample.
a. If the curve y=f(x) on the interval [a, b] is revolved about the y-axis, the area of the surface generated is ∫f(b)f(a) 2πf(y)√1+f′(y)^2 dy.
Problem 6.6.23b
Determine whether the following statements are true and give an explanation or counterexample.
b. If f is not one-to-one on the interval [a, b], then the area of the surface generated when the graph of f on [a, b] is revolved about the x-axis is not defined.
Problem 6.6.23c
Determine whether the following statements are true and give an explanation or counterexample.
c. Let f(x)=12x^2. The area of the surface generated when the graph of f on [−4, 4] is revolved about the x-axis is twice the area of the surface generated when the graph of f on [0, 4] is revolved about the x-axis.
Problem 6.6.23d
Determine whether the following statements are true and give an explanation or counterexample.
d. Let f(x)=12x^2.. The area of the surface generated when the graph of f on [−4, 4] is revolved about the y-axis is twice the area of the surface generated when the graph of f on [0, 4] is revolved about the y-axis.
Problem 6.6.25b
Consider the following curves on the given intervals.
b. Use a calculator or software to approximate the surface area.
y=cos x, for 0≤x≤π/2; about the x-axis
Problem 6.6.27a
Consider the following curves on the given intervals.
a. Write the integral that gives the area of the surface generated when the curve is revolved about the given axis.
y=tan x , for 0≤x≤π/4; about the x-axis
Problem 6.6.27b
Consider the following curves on the given intervals.
b. Use a calculator or software to approximate the surface area.
y=tan x , for 0≤x≤π/4; about the x-axis
Problem 6.6.31
Find the area of the surface generated when the given curve is revolved about the given axis.
y=x^3/2−x^1/2 / 3, for 1≤x≤2; about the x-axis
Problem 6.6.39a
In the design of solid objects (both artificial and natural), the ratio of the surface area to the volume of the object is important. Animals typically generate heat at a rate proportional to their volume and lose heat at a rate proportional to their surface area. Therefore, animals with a low SAV ratio tend to retain heat, whereas animals with a high SAV ratio (such as children and hummingbirds) lose heat relatively quickly.
a. What is the SAV ratio of a cube with side lengths a?
Problem 6.6.39b
In the design of solid objects (both artificial and natural), the ratio of the surface area to the volume of the object is important. Animals typically generate heat at a rate proportional to their volume and lose heat at a rate proportional to their surface area. Therefore, animals with a low SAV ratio tend to retain heat, whereas animals with a high SAV ratio (such as children and hummingbirds) lose heat relatively quickly.
b. What is the SAV ratio of a ball with radius a?
Problem 6.6.35
Find the area of the surface generated when the given curve is revolved about the given axis.
x=4y^3/2−y^1/2 / 12, for 1≤y≤4; about the y-axis
Problem 6.7.27a
Calculating work for different springs Calculate the work required to stretch the following springs 0.5m from their equilibrium positions. Assume Hooke’s law is obeyed.
a. A spring that requires a force of 50 N to be stretched 0.2 m from its equilibrium position
Problem 6.7.2
Explain how to find the mass of a one-dimensional object with a variable density ρ.
Problem 6.7.5
Why is integration used to find the work required to pump water out of a tank?
Problem 6.7.9
9–12. Consider the cylindrical tank in Example 4 that has a height of 10 m and a radius of 5 m. Recall that if the tank is full of water, then ∫₀¹⁰ 25 π ρg(15−y) dy equals the work required to pump all the water out of the tank, through an outflow pipe that is 15 m above the bottom of the tank. Revise this work integral for the following scenarios. (Do not evaluate the integrals.)
The work required to empty the top half of the tank
Problem 6.7.11
9–12. Consider the cylindrical tank in Example 4 that has a height of 10 m and a radius of 5 m. Recall that if the tank is full of water, then ∫₀¹⁰ 25 π ρg(15−y) dy equals the work required to pump all the water out of the tank, through an outflow pipe that is 15 m above the bottom of the tank. Revise this work integral for the following scenarios. (Do not evaluate the integrals.)
The work required to empty the tank through an outflow pipe at the top of the tank
Problem 6.7.36a
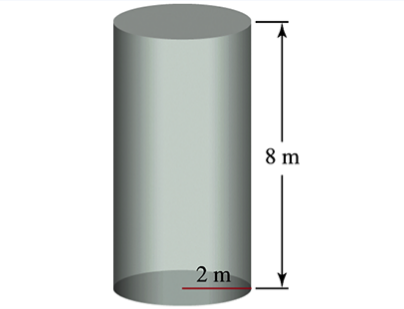
Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2m (see figure).
a. If the tank is full of water, how much work is required to pump the water to the level of the top of the tank and out of the tank?
Problem 6.7.36b
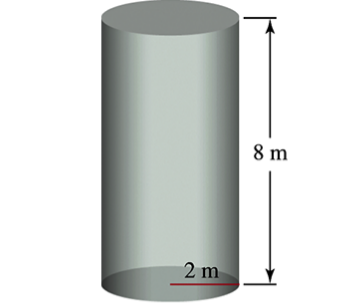
Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2m (see figure).
b. Is it true that it takes half as much work to pump the water out of the tank when it is half full as when it is full? Explain.
Problem 6.7.13
13–20. Mass of one-dimensional objects Find the mass of the following thin bars with the given density function.
ρ(x)=1+sin x, for 0≤x≤π
Problem 6.7.16
13–20. Mass of one-dimensional objects Find the mass of the following thin bars with the given density function.
ρ(x) = 5e^-2x,for 0≤x≤4
Problem 6.7.18
13–20. Mass of one-dimensional objects Find the mass of the following thin bars with the given density function.
ρ(x) = {1 if 0≤x≤2 {2 if 2<x≤3
Problem 6.7.20
13–20. Mass of one-dimensional objects Find the mass of the following thin bars with the given density function.
ρ(x) = {x² if 0≤x≤1 {x(2-x) if 1<x≤2
Problem 6.7.21
Work from force How much work is required to move an object from x=0 to x=3 (measured in meters) in the presence of a force (in N) given by F(x)=2x acting along the x-axis?
Problem 6.7.22
Work from force How much work is required to move an object from x=1 to x=3 (measured in meters) in the presence of a force (in N) given by F(x) = 2x² acting along the x-axis?
Problem 6.7.23c
Compressing and stretching a spring Suppose a force of 30 N is required to stretch and hold a spring 0.2 m from its equilibrium position.
c. How much work is required to stretch the spring 0.3 m from its equilibrium position?