Compressing and stretching a spring Suppose a force of 30 N is required to stretch and hold a spring 0.2 m from its equilibrium position.

d. How much additional work is required to stretch the spring 0.2m if it has already been stretched 0.2m from its equilibrium position?

Compressing and stretching a spring Suppose a force of 15 N is required to stretch and hold a spring 0.25 m from its equilibrium position.

b. How much work is required to compress the spring 0.2 m from its equilibrium position?

Work done by a spring A spring on a horizontal surface can be stretched and held 0.5 m from its equilibrium position with a force of 50 N.

b. How much work is done in compressing the spring 0.5 m from its equilibrium position?

Calculating work for different springs Calculate the work required to stretch the following springs 0.4 m from their equilibrium positions. Assume Hooke’s law is obeyed.

b. A spring that requires 2 J of work to be stretched 0.1 m from its equilibrium position

Calculating work for different springs Calculate the work required to stretch the following springs 1.25 m from their equilibrium positions. Assume Hooke’s law is obeyed.

a. A spring that requires 100 J of work to be stretched 0.5 m from its equilibrium position

Winding a chain A 30-m-long chain hangs vertically from a cylinder attached to a winch. Assume there is no friction in the system and the chain has a density of 5kg/m.

a. How much work is required to wind the entire chain onto the cylinder using the winch?

52–54. Force on a window A diving pool that is 4 m deep and full of water has a viewing window on one of its vertical walls. Find the force on the following windows.​ 

The window is a square, 0.5 m on a side, with the lower edge of the window on the bottom of the pool.

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

c. The work required to lift a 10-kg object vertically 10 m is the same as the work required to lift a 20-kg object vertically 5 m.

Mass of two bars Two bars of length L have densities ρ₁(x) = 4e^−x and ρ₂(x) = 6e^−2x, for 0≤x≤L.

a. For what values of L is bar 1 heavier than bar 2?

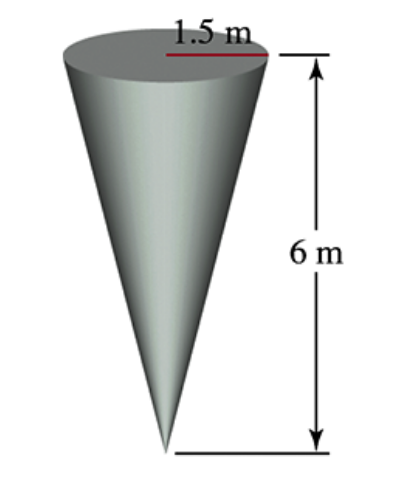
Emptying a conical tank A water tank is shaped like an inverted cone with height 6 m and base radius 1.5 m (see figure).

a. If the tank is full, how much work is required to pump the water to the level of the top of the tank and out of the tank?

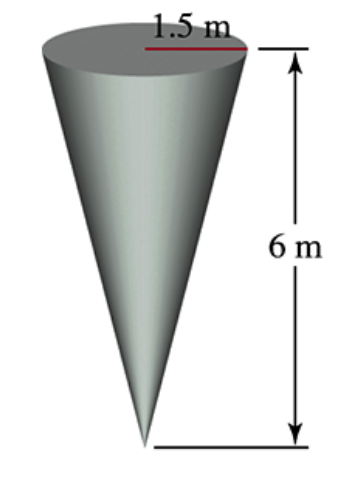
Emptying a conical tank A water tank is shaped like an inverted cone with height 6 m and base radius 1.5 m (see figure).

b. Is it true that it takes half as much work to pump the water out of the tank when it is filled to half its depth as when it is full? Explain.

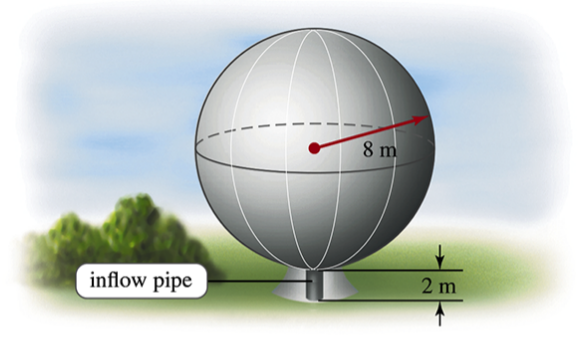
Filling a spherical tank A spherical water tank with an inner radius of 8 m has its lowest point 2 m above the ground. It is filled by a pipe that feeds the tank at its lowest point (see figure). Neglecting the volume of the inflow pipe, how much work is required to fill the tank if it is initially empty?

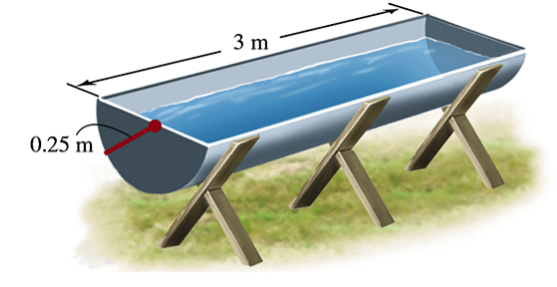
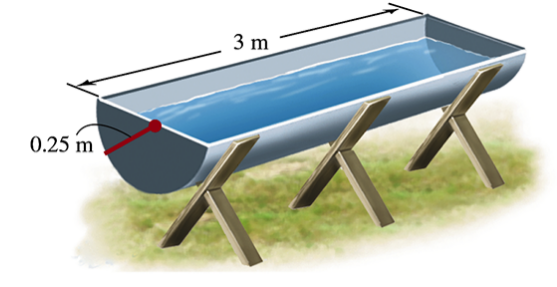
Emptying a water trough A water trough has a semicircular cross section with a radius of 0.25 m and a length of 3 m (see figure).

a. How much work is required to pump the water out of the trough (to the level of the top of the trough) when it is full?

Emptying a water trough A water trough has a semicircular cross section with a radius of 0.25 m and a length of 3 m (see figure).

b. If the length is doubled, is the required work doubled? Explain.

Emptying a water trough A water trough has a semicircular cross section with a radius of 0.25 m and a length of 3 m (see figure).

c. If the radius is doubled, is the required work doubled? Explain.

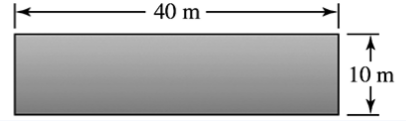
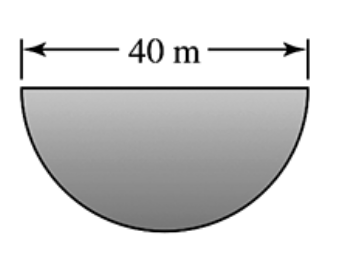
46–50. Force on dams The following figures show the shapes and dimensions of small dams. Assuming the water level is at the top of the dam, find the total force on the face of the dam.​

A nonlinear spring Hooke’s law is applicable to idealized (linear) springs that are not stretched or compressed too far from their equilibrium positions. Consider a nonlinear spring whose restoring force is given by F(x) = 16x−0.1x³, for |x|≤7. 

b. How much work is done in stretching the spring from its equilibrium position (x=0) to x=1.5?

A nonlinear spring Hooke’s law is applicable to idealized (linear) springs that are not stretched or compressed too far from their equilibrium positions. Consider a nonlinear spring whose restoring force is given by F(x) = 16x−0.1x³, for |x|≤7. 

c. How much work is done in compressing the spring from its equilibrium position (x=0) to x=−2?

Work in a gravitational field For large distances from the surface of Earth, the gravitational force is given by F(x) = GMm / (x+R)², where G = 6.7×10^−11 N m²/kg² is the gravitational constant, M = 6×10^24 kg is the mass of Earth, m is the mass of the object in the gravitational field, R = 6.378×10⁶ m is the radius of Earth, and x≥0 is the distance above the surface of Earth (in meters).

a. How much work is required to launch a rocket with a mass of 500 kg in a vertical flight path to a height of 2500 km (from Earth’s surface)?

46–50. Force on dams The following figures show the shapes and dimensions of small dams. Assuming the water level is at the top of the dam, find the total force on the face of the dam.​

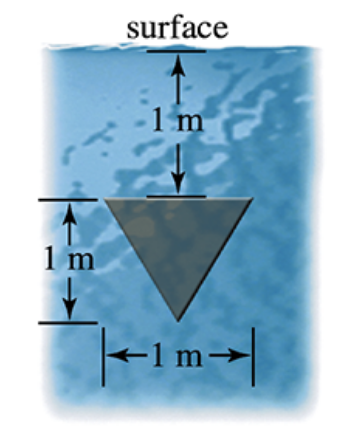
Force on a triangular plate A plate shaped like an isosceles triangle with a height of 1 m is placed on a vertical wall 1 m below the surface of a pool filled with water (see figure). Compute the force on the plate.

What is the pressure on a horizontal surface with an area of 2 m² that is 4 m underwater?

Emptying a partially filled swimming pool If the water in the swimming pool in Exercise 35 is 2 m deep, then how much work is required to pump all the water to a level 3 m above the bottom of the pool?

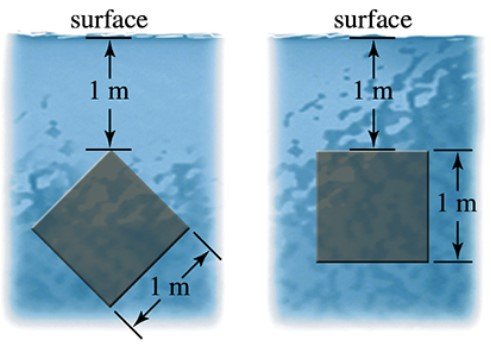
Orientation and force A plate shaped like an equilateral triangle 1 m on a side is placed on a vertical wall 1 m below the surface of a pool filled with water. On which plate in the figure is the force greater? Try to anticipate the answer and then compute the force on each plate.

Drinking juice A glass has circular cross sections that taper (linearly) from a radius of 5 cm at the top of the glass to a radius of 4 cm at the bottom. The glass is 15 cm high and full of orange juice. How much work is required to drink all the juice through a straw if your mouth is 5 cm above the top of the glass? Assume the density of orange juice equals the density of water.

Critical depth A large tank has a plastic window on one wall that is designed to withstand a force of 90,000 N. The square window is 2 m on a side, and its lower edge is 1 m from the bottom of the tank.

a. If the tank is filled to a depth of 4 m, will the window withstand the resulting force?

Winding a chain A 30-m-long chain hangs vertically from a cylinder attached to a winch. Assume there is no friction in the system and the chain has a density of 5kg/m.

b. How much work is required to wind the chain onto the cylinder if a 50-kg block is attached to the end of the chain?

Leaky Bucket A 1-kg bucket resting on the ground contains 3 kg of water. How much work is required to raise the bucket vertically a distance of 10 m if water leaks out of the bucket at a constant rate of 1/5 kg/m? Assume the weight of the rope used to raise the bucket is negligible. (Hint: Use the definition of work, W = ∫a^bF(y) dy, where F is the variable force required to lift an object along a vertical line from y=a to y=b.)

A vertical spring A 10-kg mass is attached to a spring that hangs vertically and is stretched 2 m from the equilibrium position of the spring. Assume a linear spring with F(x) = kx.

a. How much work is required to compress the spring and lift the mass 0.5 m?

52–54. Force on a window A diving pool that is 4 m deep and full of water has a viewing window on one of its vertical walls. Find the force on the following windows.​ 

The window is circular, with a radius of 0.5 m, tangent to the bottom of the pool.