43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.

The region bounded by the curves y = sec x and y=2, for 0 ≤ x ≤ π/3, is revolved about the x-axis. What is the volume of the solid that is generated? 

82–84. Fluid Forces Suppose the following plates are placed on a vertical wall so that the top of the plate is 2 m below the surface of a pool that is filled with water. Compute the force on each plate.

​​A circular plate with a radius of 2 m

43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.

The region bounded by the graph of y = 4−x² and the x-axis on the interval [−2,2] is revolved about the line x = −2. What is the volume of the solid that is generated?

43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.

The region bounded by the graphs of y = 2x,y = 6−x, and y = 0 is revolved about the line y = −2 and the line x = −2. Find the volumes of the resulting solids. Which one is greater?

43–55. Volumes of solids Choose the general slicing method, the disk/washer method, or the shell method to answer the following questions.

The region bounded by the graphs of y = 2x,y = 6−x, and y = 0 is revolved about the line y = −2 and the line x = −2. Find the volumes of the resulting solids. Which one is greater?

Comparing volumes Let R be the region bounded by y=1/x^p and the x-axis on the interval [1, a], where p>0 and a>1 (see figure). Let Vₓ and Vᵧ be the volumes of the solids generated when R is revolved about the x- and y-axes, respectively.

c. Find a general expression for Vₓ in terms of a and p. Note that p=1/2 is a special case. What is Vₓ when p=1/2?

Comparing volumes Let R be the region bounded by y=1/x^p and the x-axis on the interval [1, a], where p>0 and a>1 (see figure). Let Vₓ and Vᵧ be the volumes of the solids generated when R is revolved about the x- and y-axes, respectively.

d. Find a general expression for Vᵧ in terms of a and p. Note that p=2 is a special case. What is Vᵧ when p=2?

Force on a dam Find the total force on the face of a semicircular dam with a radius of 20 m when its reservoir is full of water. The diameter of the semicircle is the top of the dam.

58–61. Arc length Find the length of the following curves.​

y = x³/6 + 1/2x on [1,2]

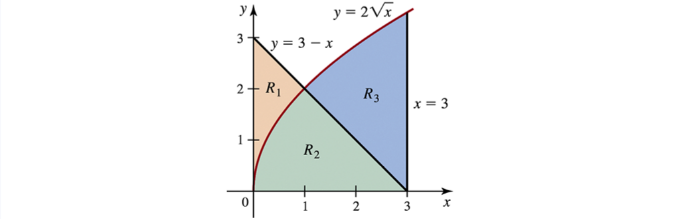
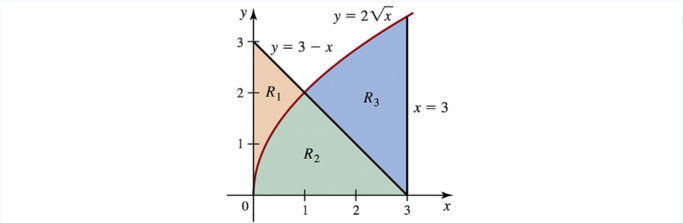
27–33. Multiple regions The regions R₁,R₂, and R₃ (see figure) are ​formed by​ the graphs of y = 2√x,y = 3−x,and x=3.

​ Use the shell method to find an integral, or sum of integrals, that equals the volume of the solid obtained by revolving region R₃ about the line x=3. Do not evaluate the integral.

27–33. Multiple regions The regions R₁,R₂, and R₃ (see figure) are ​formed by​ the graphs of y = 2√x,y = 3−x,and x=3.

​ Find the volume of the solid obtained by revolving region R₂ about the y-axis.

40–43. Population growth

A culture of bacteria in a Petri dish has an initial population of 1500 cells and grows at a rate (in cells/day) of N′(t) = 100e^−0.25t. Assume t is measured in days.

a. What is the population after 20 days? After 40 days?​​

Acceleration A drag racer accelerates at a(t)=88 ft/s². Assume v(0)=0, s(0)=0, and t is measured in seconds.

c. At this rate, how long will it take the racer to travel 1/4 mi?

29–36. Position and velocity from acceleration Find the position and velocity of an object moving along a straight line with the given acceleration, initial velocity, and initial position. Use the Fundamental Theorem of Calculus (Theorems 6.1 and 6.2).

a(t) = cos2t; v(0) = 5; s(0) = 7

29–36. Position and velocity from acceleration Find the position and velocity of an object moving along a straight line with the given acceleration, initial velocity, and initial position. Use the Fundamental Theorem of Calculus (Theorems 6.1 and 6.2).

a(t) = e^−t; v(0) = 60; s(0) = 40

29–36. Position and velocity from acceleration Find the position and velocity of an object moving along a straight line with the given acceleration, initial velocity, and initial position. Use the Fundamental Theorem of Calculus (Theorems 6.1 and 6.2).

a(t) = −32; v(0)=50; s(0)=0

Probe speed A data collection probe is dropped from a stationary balloon, and it falls with a velocity (in m/s) given by v(t) = 9.8t, neglecting air resistance. After 10 s, a chute deploys and the probe immediately slows to a constant speed of 10 m/s, which it maintains until it enters the ocean.

c. If the probe was released from an altitude of 3 km, when does it enter the ocean?

Probe speed A data collection probe is dropped from a stationary balloon, and it falls with a velocity (in m/s) given by v(t) = 9.8t, neglecting air resistance. After 10 s, a chute deploys and the probe immediately slows to a constant speed of 10 m/s, which it maintains until it enters the ocean.

b. How far does the probe fall in the first 30 s after it is released?

Day hike The velocity (in mi/hr) of a hiker walking along a straight trail is given by v(t) = 3 sin² πt/2, for 0≤t≤4. Assume s(0)=0 and t is measured in hours. 

c. What is the hiker’s position at t=3?

Flying into a headwind The velocity (in mi/hr) of an airplane flying into a headwind is given by v(t) = 30(16−t²), for 0≤t≤3. Assume s(0)=0 and t is measured in hours.

c. How far has the airplane traveled at the instant its velocity reaches 400 mi/hr?

​​​​​​​​​​​​​​​​​​​​​​​​Cycling distance A cyclist rides down a long straight road with a velocity (in m/min) given by v(t) = 400−20t, for 0≤t≤10, where t is measured in minutes.

c. How far has the cyclist traveled when her velocity is 250 m/min?

​​​​​​​​​​​​​​​​​​​​​​​​Cycling distance A cyclist rides down a long straight road with a velocity (in m/min) given by v(t) = 400−20t, for 0≤t≤10, where t is measured in minutes.

b. How far does the cyclist travel in the first 10 min?

17–22. Position from velocity Consider an object moving along a line with the given velocity v and initial position.

a. Determine the position function, for t≥0, using the antiderivative method

v(t) = 9−t² on [0, 4]; s(0)=−2

17–22. Position from velocity Consider an object moving along a line with the given velocity v and initial position.

a. Determine the position function, for t≥0, using the antiderivative method

v(t) = 6−2t on [0, 5]; s(0)=0

17–22. Position from velocity Consider an object moving along a line with the given velocity v and initial position.

a. Determine the position function, for t≥0, using the antiderivative method

v(t) = −t³+3t²−2t on [0, 3]; s(0)=4

13–16. Displacement from velocity Consider an object moving along a line with the given velocity v. Assume time t is measured in seconds and velocities have units of m/s.

b. Find the displacement over the given interval. 

v(t) = 50e^−2t on [0, 4]​​

13–16. Displacement from velocity Consider an object moving along a line with the given velocity v. Assume time t is measured in seconds and velocities have units of m/s.

a. Determine when the motion is in the positive direction and when it is in the negative direction. 

v(t) = 50e^−2t on [0, 4]​​

13–16. Displacement from velocity Consider an object moving along a line with the given velocity v. Assume time t is measured in seconds and velocities have units of m/s.

c. Find the distance traveled over the given interval.

v(t) = 4t³ - 24t²+20t on [0, 5]

13–16. Displacement from velocity Consider an object moving along a line with the given velocity v. Assume time t is measured in seconds and velocities have units of m/s.

c. Find the distance traveled over the given interval.

v(t) = 3t²−6t on [0, 3]

13–16. Displacement from velocity Consider an object moving along a line with the given velocity v. Assume time t is measured in seconds and velocities have units of m/s.

b. Find the displacement over the given interval. 

v(t) = 3t²−6t on [0, 3]