Back
BackProblem 6.1.64c
Where do they meet? Kelly started at noon (t=0) riding a bike from Niwot to Berthoud, a distance of 20 km, with velocity v(t) = 15 / (t + 1)² (decreasing because of fatigue). Sandy started at noon (t=0) riding a bike in the opposite direction from Berthoud to Niwot with velocity u(t) = 20 / (t + 1)² (also decreasing because of fatigue). Assume distance is measured in kilometers and time is measured in hours.
c. When do they meet? How far has each person traveled when they meet?
Problem 6.1.64d
Where do they meet? Kelly started at noon (t=0) riding a bike from Niwot to Berthoud, a distance of 20 km, with velocity v(t) = 15 / (t + 1)² (decreasing because of fatigue). Sandy started at noon (t=0) riding a bike in the opposite direction from Berthoud to Niwot with velocity u(t) = 20 / (t + 1)² (also decreasing because of fatigue). Assume distance is measured in kilometers and time is measured in hours.
d. More generally, if the riders’ speeds are v(t)=A(t+1)² and u(t)=B(t+1)² and the distance between the towns is D, what conditions on A, B, and D must be met to ensure that the riders will pass each other?
Problem 6.1.65a
Bike race Theo and Sasha start at the same place on a straight road, riding bikes with the following velocities (measured in mi/hr). Assume t is measured in hours.
Theo: vT(t)=10, for t≥0
Sasha: vS(t)=15t, for 0≤t≤1, and vS(t)=15, for t>1
a. Graph the velocity function for both riders.
Problem 6.1.65c
Bike race Theo and Sasha start at the same place on a straight road, riding bikes with the following velocities (measured in mi/hr). Assume t is measured in hours.
Theo: vT(t)=10, for t≥0
Sasha: vS(t)=15t, for 0≤t≤1, and vS(t)=15, for t>1
c. If the riders ride for 2 hr, who rides farther? Interpret your answer geometrically using the graphs of part (a).
Problem 6.1.65f
Bike race Theo and Sasha start at the same place on a straight road, riding bikes with the following velocities (measured in mi/hr). Assume t is measured in hours.
Theo: vT(t)=10, for t≥0
Sasha: vS(t)=15t, for 0≤t≤1, and vS(t)=15, for t>1
f. Suppose Sasha gives Theo a head start of 0.2 hr and the riders ride for 20 mi. Who wins the race?
Problem 6.1.66b
Two runners At noon (t=0), Alicia starts running along a long straight road at 4 mi/hr. Her velocity decreases according to the function v(t) = 4 / t + 1 for t≥0. At noon, Boris also starts running along the same road with a 2-mi head start on Alicia; his velocity is given by u(t) = 2 / t + 1, for t≥0. Assume t is measured in hours.
b. When, if ever, does Alicia overtake Boris?
Problem 6.1.7a
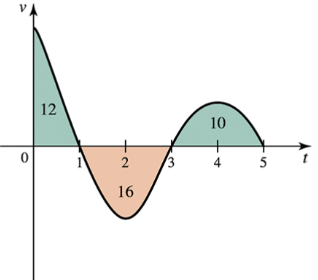
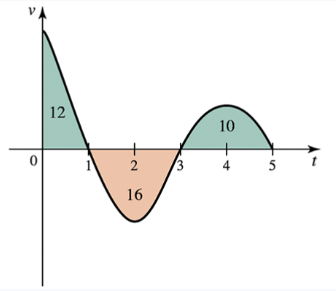
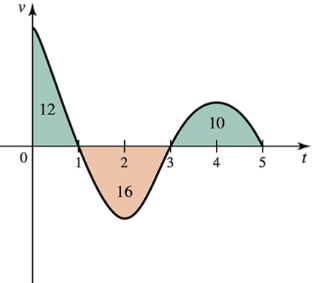
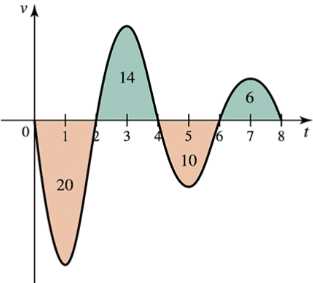
Displacement and distance from velocity Consider the graph shown in the figure, which gives the velocity of an object moving along a line. Assume time is measured in hours and distance is measured in miles. The areas of three regions bounded by the velocity curve and the t-axis are also given.
a. On what intervals is the object moving in the positive direction?
Problem 6.1.7b
Displacement and distance from velocity Consider the graph shown in the figure, which gives the velocity of an object moving along a line. Assume time is measured in hours and distance is measured in miles. The areas of three regions bounded by the velocity curve and the t-axis are also given.
b. What is the displacement of the object over the interval [0,3]?
Problem 6.1.7d
Displacement and distance from velocity Consider the graph shown in the figure, which gives the velocity of an object moving along a line. Assume time is measured in hours and distance is measured in miles. The areas of three regions bounded by the velocity curve and the t-axis are also given.
d. What is the displacement of the object over the interval [0,5]?
Problem 6.1.8b
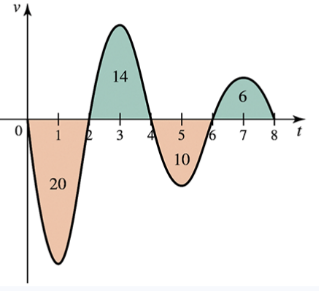
Displacement and distance from velocity Consider the velocity function shown below of an object moving along a line. Assume time is measured in seconds and distance is measured in meters. The areas of four regions bounded by the velocity curve and the t-axis are also given.
b. What is the displacement of the object over the interval [2, 6]?
Problem 6.1.8d
Displacement and distance from velocity Consider the velocity function shown below of an object moving along a line. Assume time is measured in seconds and distance is measured in meters. The areas of four regions bounded by the velocity curve and the t-axis are also given.
d. What is the displacement of the object over the interval [0, 8]?
Problem 6.1.8e
Displacement and distance from velocity Consider the velocity function shown below of an object moving along a line. Assume time is measured in seconds and distance is measured in meters. The areas of four regions bounded by the velocity curve and the t-axis are also given.
e. Describe the position of the object relative to its initial position after 8 seconds.
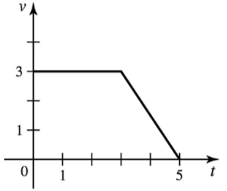
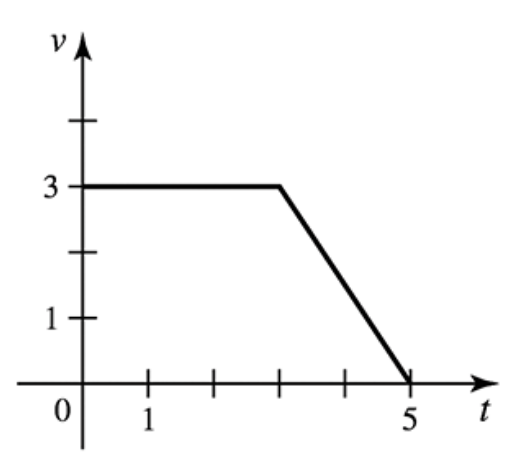
Problem 6.1.9a
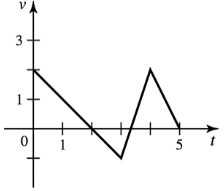
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
a. The displacement between t=0 and t=5
Problem 6.1.9d
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
d. A piecewise function for s(t)
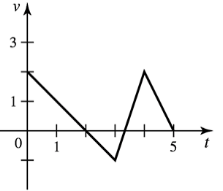
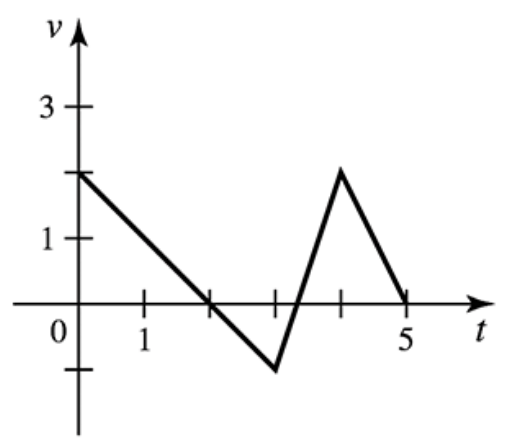
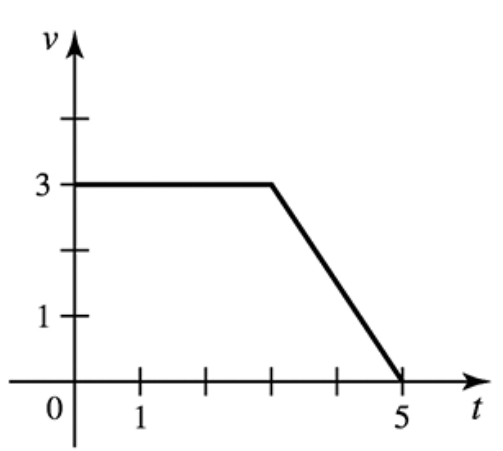
Problem 6.1.10a
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
a. The displacement between t=0 and t=5
Problem 6.1.10c
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
c. The position at t=5
Problem 6.1.23a
{Use of Tech} Oscillating motion A mass hanging from a spring is set in motion, and its ensuing velocity is given by v(t) = 2π cos πt, for t≥0. Assume the positive direction is upward and s(0)=0.
a. Determine the position function, for t≥0.
Problem 6.1.23c
{Use of Tech} Oscillating motion A mass hanging from a spring is set in motion, and its ensuing velocity is given by v(t) = 2π cos πt, for t≥0. Assume the positive direction is upward and s(0)=0.
c. At what times does the mass reach its low point the first three times?
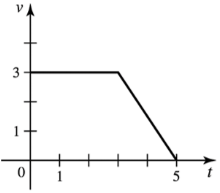
Problem 6.1.27c
Piecewise velocity The velocity of a (fast) automobile on a straight highway is given by the function
, where is measured in seconds and v has units of m/s.
c. What is the distance traveled by the automobile in the first 60 s?
Problem 6.1.68b
Variable gravity At Earth’s surface, the acceleration due to gravity is approximately g=9.8 m/s² (with local variations). However, the acceleration decreases with distance from the surface according to Newton’s law of gravitation. At a distance of y meters from Earth’s surface, the acceleration is given by a(y) = - g / (1+y/R)², where R=6.4×10⁶ m is the radius of Earth.
b. Use the Chain Rule to show that dv/dt = 1/2 d/dy(v²).
Problem 6.1.9c
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
c. The position at t=5
Problem 6.1.10b
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
b. The distance traveled between t=0 and t=5
Problem 6.1.10d
9–10. Velocity graphs The figures show velocity functions for motion along a line. Assume the motion begins with an initial position of s(0)=0. Determine the following.
d. A piecewise function for s(t)
Problem 6.1.27d
Piecewise velocity The velocity of a (fast) automobile on a straight highway is given by the function
where is measured in seconds and v has units of m/s.
d. What is the position of the automobile when t=75?
Problem 6.1.46a
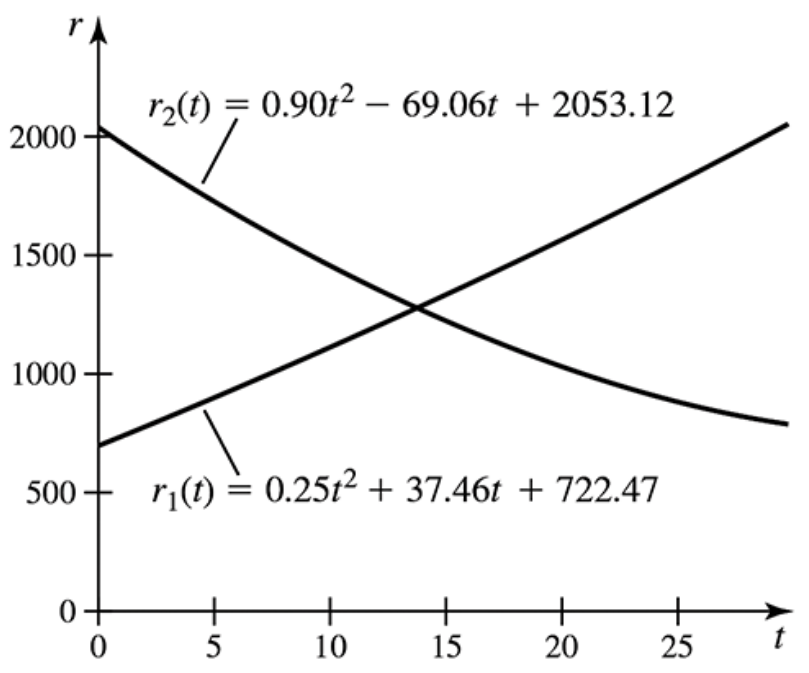
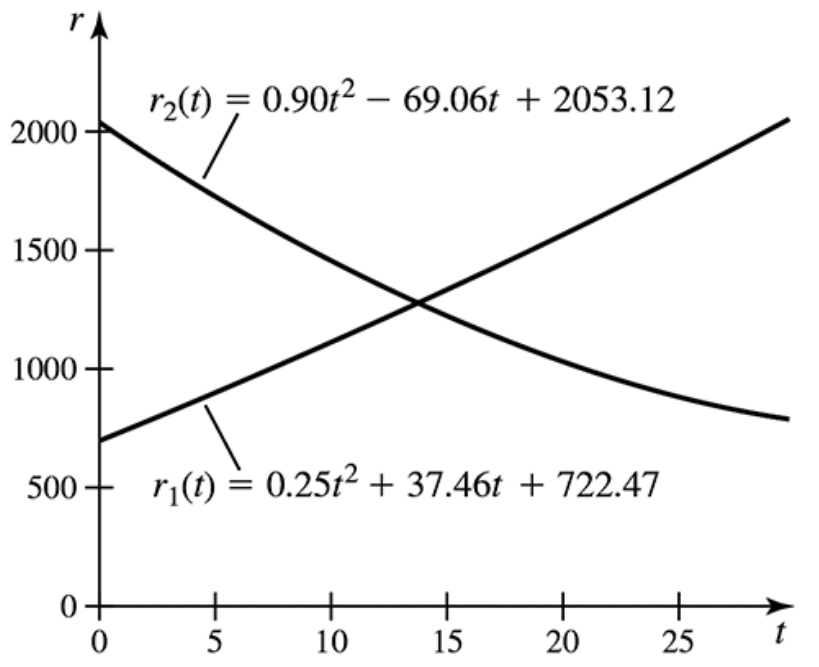
Flow rates in the Spokane River The daily discharge of the Spokane River as it flows through Spokane, Washington, in April and June is modeled by the functions
r1(t) = 0.25t²+37.46t+722.47 (April) and
r2(t) = 0.90t²−69.06t+2053.12 (June), where the discharge is measured in millions of cubic feet per day, and t=0 corresponds to the beginning of the first day of the month (see figure).
a. Determine the total amount of water that flows through Spokane in April (30 days).
Problem 6.1.46c
Flow rates in the Spokane River The daily discharge of the Spokane River as it flows through Spokane, Washington, in April and June is modeled by the functions
r1(t) = 0.25t²+37.46t+722.47 (April) and
r2(t) = 0.90t²−69.06t+2053.12 (June), where the discharge is measured in millions of cubic feet per day, and t=0 corresponds to the beginning of the first day of the month (see figure).
c. The Spokane River flows out of Lake Coeur d’Alene, which contains approximately 0.67mi³ of water. Determine the percentage of Lake Coeur d’Alene’s volume that flows through Spokane in April and June.
Problem 6.1.69
Suppose f and g have continuous derivatives on an interval [a, b]. Prove that if f(a)=g(a) and f(b)=g(b), then ∫a^b f′(x) dx = ∫a^b g′(x) dx.
Problem 6.1.72
Without evaluating integrals, prove that ∫₀² d/dx(12 sin πx²) dx=∫₀² d/dx (x¹⁰(2−x)³) dx.
Problem 6.2.9
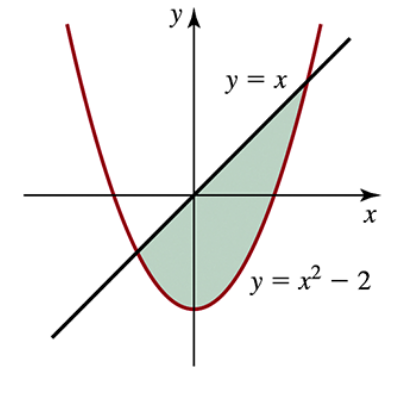
Determine the area of the shaded region in the following figures.
Problem 6.2.15
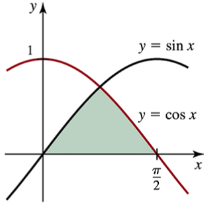
Determine the area of the shaded region in the following figures.