Back
BackProblem 6.2.51
Find the area of the region described in the following exercises.
The region bounded by y=e^x, y=2e^−x+1, and x=0
Problem 6.2.11
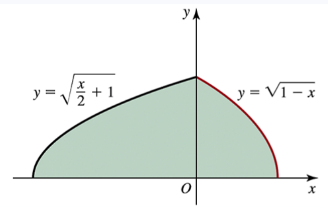
Determine the area of the shaded region in the following figures.
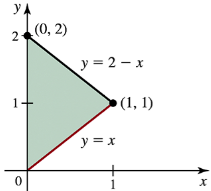
Problem 6.2.13
Determine the area of the shaded region in the following figures.
(Hint: Find the intersection point by inspection.)
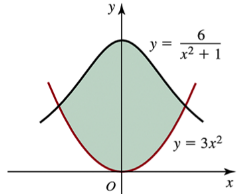
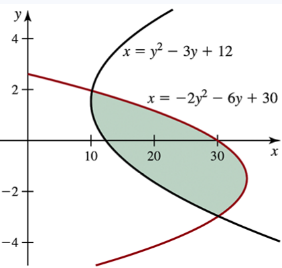
Problem 6.2.17
Determine the area of the shaded region in the following figures.
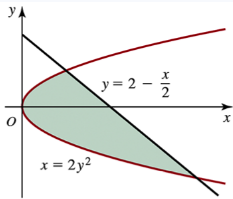
Problem 6.2.19
Determine the area of the shaded region in the following figures.
Problem 6.2.37
Find the area of the region described in the following exercises.
The region bounded by y=4x+4, y=6x+6, and x=4
Problem 6.2.39
Find the area of the region described in the following exercises.
The region bounded by y=e^x, y=e^−2x, and x=ln 4
Problem 6.2.41
Find the area of the region described in the following exercises.
The region bounded by y=2 / 1 + x^2 and y=1
Problem 6.2.45
Find the area of the region described in the following exercises.
The region bounded by y=2−|x|and y=x^2
Problem 6.2.47
Find the area of the region described in the following exercises.
The region bounded by y=|x−3|and y=x/2
Problem 6.2.49
Find the area of the region described in the following exercises.
The region in the first quadrant bounded by y=x^2/3 and y=4
Problem 6.2.55
Find the area of the region described in the following exercises.
The region bounded by y=√x, y=2x−15, and y=0
Problem 6.2.29
Determine the area of the shaded region in the following figures.
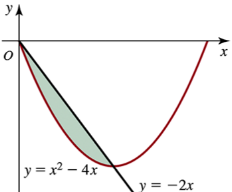
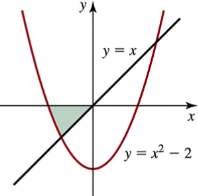
Problem 6.2.21
Determine the area of the shaded region in the following figures.
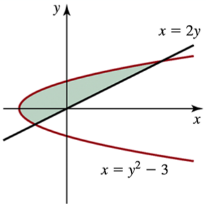
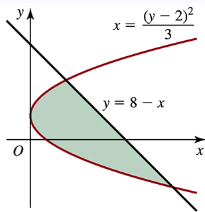
Problem 6.2.27
Determine the area of the shaded region in the following figures.
Problem 6.2.23
Determine the area of the shaded region in the following figures.
Problem 6.2.25
Determine the area of the shaded region in the following figures.
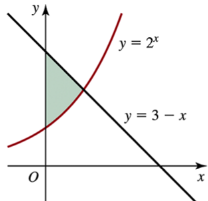
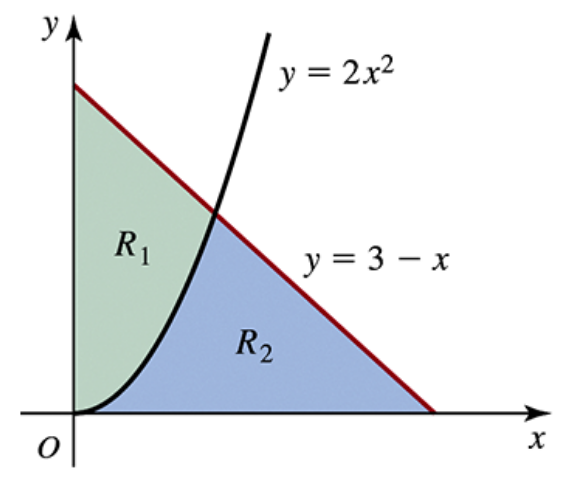
Problem 6.2.34a
For the given regions R₁ and R₂, complete the following steps.
a. Find the area of region R₁.
R₁ is the region in the first quadrant bounded by the y-axis and the curves y=2x^2 and y=3−x; R₂ is the region in the first quadrant bounded by the x-axis and the curves y=2x^2 and y=3−x(see figure).
Problem 6.2.35a
For the given regions R₁ and R₂, complete the following steps.
a. Find the area of region R₁.
R₁is the region in the first quadrant bounded by the line x=1 and the curve y=6x(2−x^2)^2; R₂ is the region in the first quadrant bounded the curve y=6x(2−x^2)^2and the line y=6x.
Problem 6.2.35b
For the given regions R₁ and R₂, complete the following steps.
b. Find the area of region R₂ using geometry and the answer to part (a).
R₁is the region in the first quadrant bounded by the line x=1 and the curve y=6x(2−x^2)^2; R₂ is the region in the first quadrant bounded the curve y=6x(2−x^2)^2and the line y=6x.
Problem 6.2.59
Find the area of the region described in the following exercises.
The region bounded by x=y(y−1) and y=x/3
Problem 6.2.61
Find the area of the region described in the following exercises.
The region in the first quadrant bounded by y=5/2−1/x and y=x
Problem 6.2.65a
Determine whether the following statements are true and give an explanation or counterexample.
a. The area of the region bounded by y=x and x=y^2 can be found only by integrating with respect to x.
Problem 6.2.65b
Determine whether the following statements are true and give an explanation or counterexample.
b. The area of the region between y=sin x and y=cos x on the interval [0,π/2] is ∫π/20(cosx−sinx)dx.
Problem 6.2.57
Find the area of the region described in the following exercises.
The region bounded by y=x^2−2x+1 and y=5x−9
Problem 6.2.65c
Determine whether the following statements are true and give an explanation or counterexample.
c. ∫₀¹(x−x^2) dx=∫₀¹(√y−y) dy
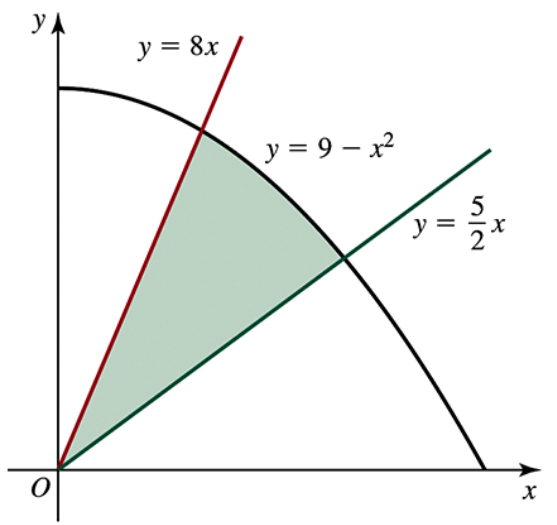
Problem 6.2.63
Find the area of the shaded regions in the following figures.
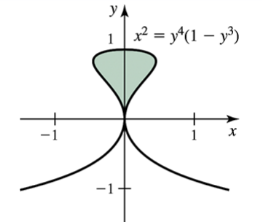
Problem 6.2.71
Determine the area of the shaded region bounded by the curve x^2=y^4(1−y^3) (see figure).
Problem 6.2.E.71
Find the area of the following regions, expressing your results in terms of the positive integer n≥2.
Let Aₙ be the area of the region bounded by f(x)=x^1/n and g(x)=x^n on the interval [0,1], where n is a positive integer. Evaluate lim n→∞ Aₙ and interpret the result. br
Problem 6.2.7
Express the area of the shaded region in Exercise 5 as the sum of two integrals with respect to y. Do not evaluate the integrals.