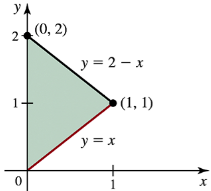
Find the area of the region (see figure) in two ways.

a. Using integration with respect to x.

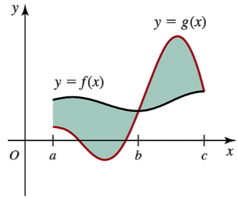
Set up a sum of two integrals that equals the area of the shaded region bounded by the graphs of the functions f and g on [a, c] (see figure). Assume the curves intersect at x=b.

Consider the region R in the first quadrant bounded by y=x^1/n and y=x^n, where n>1 is a positive number.

a. Find the volume V(n) of the solid generated when R is revolved about the x-axis. Express your answer in terms of n.

Use the region R that is bounded by the graphs of y=1+√x,x=4, and y=1 complete the exercises.

Region R is revolved about the x-axis to form a solid of revolution whose cross sections are washers.

b. What is the inner radius of a cross section of the solid at a point x in [0, 4]?​​

Use the region R that is bounded by the graphs of y=1+√x,x=4, and y=1 complete the exercises.

Region R is revolved about the x-axis to form a solid of revolution whose cross sections are washers.

d. Write an integral for the volume of the solid.

Use the region R that is bounded by the graphs of y=1+√x,x=4, and y=1 complete the exercises.

Region R is revolved about the y-axis to form a solid of revolution whose cross sections are washers.

b. What is the inner radius of a cross section of the solid at a point y in [1, 3]?

Use the region R that is bounded by the graphs of y=1+√x,x=4, and y=1 complete the exercises.

Region R is revolved about the y-axis to form a solid of revolution whose cross sections are washers.

c. What is the area A(y) of a cross section of the solid at a point y in [1, 3]?

Use the region R that is bounded by the graphs of y=1+√x,x=4, and y=1 complete the exercises.

Region R is revolved about the y-axis to form a solid of revolution whose cross sections are washers.

d. Write an integral for the volume of the solid.

Region R is revolved about the line y=1 to form a solid of revolution.

a. What is the radius of a cross section of the solid at a point x in [0, 4]?

Region R is revolved about the line y=1 to form a solid of revolution.

c. Write an integral for the volume of the solid.

Region R is revolved about the line x=4 to form a solid of revolution.

a. What is the radius of a cross section of the solid at a point y in [1, 3]?

For the following regions R, determine which is greater—the volume of the solid generated when R is revolved about the x-axis or about the y-axis.

R is bounded by y=4−2x, the x-axis, and the y-axis.​​

For the following regions R, determine which is greater—the volume of the solid generated when R is revolved about the x-axis or about the y-axis.

R is bounded by y=1−x^3, the x-axis, and the y-axis.

For the following regions R, determine which is greater—the volume of the solid generated when R is revolved about the x-axis or about the y-axis.

R is bounded by y=x^2 and y=√8x.

Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given line.

x=2−secy,x=2,y=π/3, and y=0; about x=2

Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given line.

y=2 sin x and y=0 on [0,π]; about y=−2

Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given line.

y=x and y=1+x/2; about y=3

The region R is bounded by the graph of f(x)=2x(2−x) and the x-axis. Which is greater, the volume of the solid generated when R is revolved about the line y=2 or the volume of the solid generated when R is revolved about the line y=0? Use integration to justify your answer.

A right circular cylinder with height R and radius R has a volume of VC=πR^3 (height = radius).

a. Find the volume of the cone that is inscribed in the cylinder with the same base as the cylinder and height R. Express the volume in terms of VC.

A right circular cylinder with height R and radius R has a volume of VC=πR^3 (height = radius).

b. Find the volume of the hemisphere that is inscribed in the cylinder with the same base as the cylinder. Express the volume in terms of VC.

A hemispherical bowl of radius 8 inches is filled to a depth of h inches, where 0≤h≤8 0 ≤ ℎ ≤ 8 . Find the volume of water in the bowl as a function of h. (Check the special cases h=0 and h=8.)

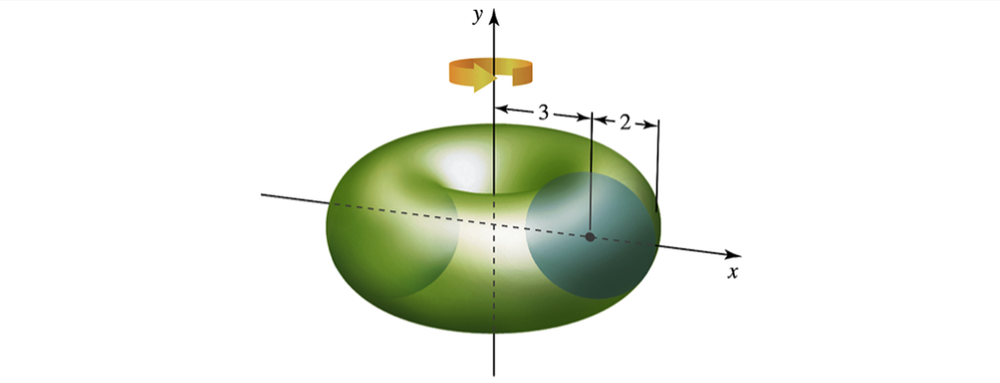
Find the volume of the torus formed when the circle of radius 2 centered at (3, 0) is revolved about the y-axis. Use geometry to evaluate the integral.​​

Suppose a cut is made through a solid object perpendicular to the x-axis at a particular point x. Explain the meaning of A(x).

A solid has a circular base; cross sections perpendicular to the base are squares. What method should be used to find the volume of the solid?​​

Consider a solid whose base is the region in the first quadrant bounded by the curve y=√3−x and the line x=2, and whose cross sections through the solid perpendicular to the x-axis are squares.

a. Find an expression for the area A(x) of a cross section of the solid at a point x in [0, 2].

Why is the disk method a special case of the general slicing method?​​

Let R be the region bounded by the curve y=√cos x and the x-axis on [0, π/2]. A solid of revolution is obtained by revolving R about the x-axis (see figures). 

c. Write an integral for the volume of the solid.

Let R be the region bounded by the curve y=cos^−1x and the x-axis on [0, 1]. A solid of revolution is obtained by revolving R about the y-axis (see figures). 

b. Find an expression for the area A(y) of a cross section of the solid at a point y in [0,π/2]. 

Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.

y=4−x^2,x=2, and y=4; about the y-axis

Use the general slicing method to find the volume of the following solids.

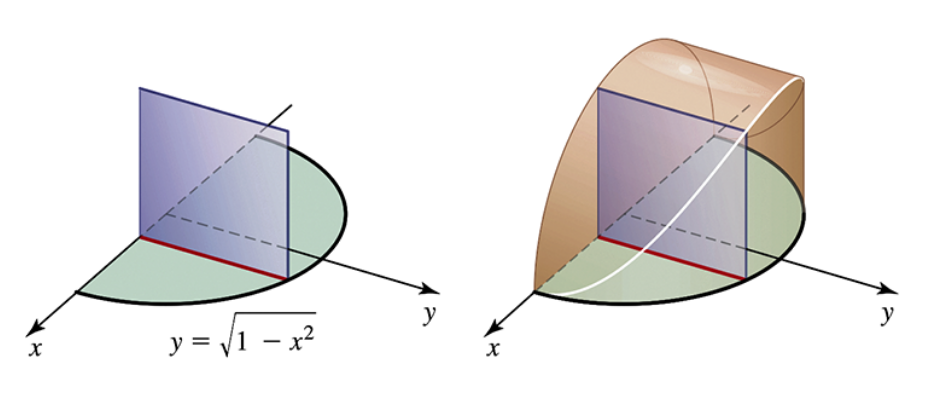
The solid whose base is the region bounded by the semicircle y=√1−x^2 and the x-axis, and whose cross sections through the solid perpendicular to the x-axis are squares​​