Back
BackProblem 10.1.5
Find two different explicit formulas for the sequence {1, -2, 3, -4, -5 .....}
Problem 10.1.29a
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
a. Find the next two terms of the sequence.
{1, 2, 4, 8, 16, ......}
Problem 10.1.31a
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
a. Find the next two terms of the sequence.
{1, 3, 9, 27, 81, ......}
Problem 10.1.33a
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
a. Find the next two terms of the sequence.
{-5, 5, -5, 5, ......}
Problem 10.1.57a
57–60. Heights of bouncing balls A ball is thrown upward to a height of hₒ meters. After each bounce, the ball rebounds to a fraction r of its previous height. Let hₙ be the height after the nth bounce. Consider the following values of hₒ and r.
a. Find the first four terms of the sequence of heights {hₙ}.
h₀ = 20, r = 0.5
Problem 10.1.59a
57–60. Heights of bouncing balls A ball is thrown upward to a height of hₒ meters. After each bounce, the ball rebounds to a fraction r of its previous height. Let hₙ be the height after the nth bounce. Consider the following values of hₒ and r.
a. Find the first four terms of the sequence of heights {hₙ}.
h₀ = 30, r = 0.25
Problem 10.1.73a
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
a. Write out the first five terms of the sequence.
Radioactive decay
A material transmutes 50% of its mass to another element every 10 years due to radioactive decay. Let Mₙ be the mass of the radioactive material at the end of the nᵗʰ decade, where the initial mass of the material is M₀ = 20g.
Problem 10.1.75a
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
a. Write out the first five terms of the sequence.
Drug elimination
Jack took a 200-mg dose of a pain killer at midnight. Every hour, 5% of the drug is washed out of his bloodstream. Let dₙ be the amount of drug in Jack’s blood n hours after the drug was taken, where d₀ = 200mg.
Problem 10.1.29b
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
b. Find a recurrence relation that generates the sequence (supply the initial value of the index and the first term of the sequence).
{1, 2, 4, 8, 16, ......}
Problem 10.1.29c
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
c. Find an explicit formula for the nth term of the sequence.
{1, 2, 4, 8, 16, ......}
Problem 10.1.31b
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
b. Find a recurrence relation that generates the sequence (supply the initial value of the index and the first term of the sequence).
{1, 3, 9, 27, 81, ......}
Problem 10.1.31c
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
c. Find an explicit formula for the nth term of the sequence.
{1, 3, 9, 27, 81, ......}
Problem 10.1.33b
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
b. Find a recurrence relation that generates the sequence (supply the initial value of the index and the first term of the sequence).
{-5, 5, -5, 5, ......}
Problem 10.1.33c
27–34. Working with sequences Several terms of a sequence {aₙ}ₙ₌₁∞ are given.
c. Find an explicit formula for the nth term of the sequence.
{-5, 5, -5, 5, ......}
Problem 10.1.57b
57–60. Heights of bouncing balls A ball is thrown upward to a height of hₒ meters. After each bounce, the ball rebounds to a fraction r of its previous height. Let hₙ be the height after the nth bounce. Consider the following values of hₒ and r.
b. Find an explicit formula for the nth term of the sequence {hₙ}.
h₀ = 20, r = 0.5
Problem 10.1.59b
57–60. Heights of bouncing balls A ball is thrown upward to a height of hₒ meters. After each bounce, the ball rebounds to a fraction r of its previous height. Let hₙ be the height after the nth bounce. Consider the following values of hₒ and r.
b. Find an explicit formula for the nth term of the sequence {hₙ}.
h₀ = 30, r = 0.25
Problem 10.1.73b
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
b. Find an explicit formula for the terms of the sequence.
Radioactive decay
A material transmutes 50% of its mass to another element every 10 years due to radioactive decay. Let Mₙ be the mass of the radioactive material at the end of the nᵗʰ decade, where the initial mass of the material is M₀ = 20g.
Problem 10.1.73c
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
c. Find a recurrence relation that generates the sequence.
Radioactive decay
A material transmutes 50% of its mass to another element every 10 years due to radioactive decay. Let Mₙ be the mass of the radioactive material at the end of the nᵗʰ decade, where the initial mass of the material is M₀ = 20g.
Problem 10.1.73d
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
d. Using a calculator or a graphing utility, estimate the limit of the sequence or state that it does not exist.
Radioactive decay
A material transmutes 50% of its mass to another element every 10 years due to radioactive decay. Let Mₙ be the mass of the radioactive material at the end of the nᵗʰ decade, where the initial mass of the material is M₀ = 20g.
Problem 10.1.75b
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
b. Find an explicit formula for the terms of the sequence.
Drug elimination
Jack took a 200-mg dose of a pain killer at midnight. Every hour, 5% of the drug is washed out of his bloodstream. Let dₙ be the amount of drug in Jack’s blood n hours after the drug was taken, where d₀ = 200mg.
Problem 10.1.75c
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
c. Find a recurrence relation that generates the sequence.
Drug elimination
Jack took a 200-mg dose of a pain killer at midnight. Every hour, 5% of the drug is washed out of his bloodstream. Let dₙ be the amount of drug in Jack’s blood n hours after the drug was taken, where d₀ = 200mg.
Problem 10.1.75d
72–75. {Use of Tech} Practical sequences
Consider the following situations that generate a sequence
d. Using a calculator or a graphing utility, estimate the limit of the sequence or state that it does not exist.
Drug elimination
Jack took a 200-mg dose of a pain killer at midnight. Every hour, 5% of the drug is washed out of his bloodstream. Let dₙ be the amount of drug in Jack’s blood n hours after the drug was taken, where d₀ = 200mg.
Problem 10.1.67a
67–70. Formulas for sequences of partial sums Consider the following infinite series.
a. Find the first four partial sums S₁, S₂, S₃, S₄ of the series.
∑⁽∞⁾ₖ₌₁ 2⁄[(2k − 1)(2k + 1)]
Problem 10.1.67c
67–70. Formulas for sequences of partial sums Consider the following infinite series.
c. Make a conjecture for the value of the series.
∑⁽∞⁾ₖ₌₁ 2⁄[(2k − 1)(2k + 1)]
Problem 10.1.71a
Explain why or why not
Determine whether the following statements are true and give an explanation or counterexample.
a. The sequence of partial sums for the series 1 + 2 + 3 + ⋯ is {1, 3, 6, 10, …}.
Problem 10.1.71b
Explain why or why not
Determine whether the following statements are true and give an explanation or counterexample.
b. If a sequence of positive numbers converges, then the sequence is decreasing.
Problem 10.1.71c
Explain why or why not
Determine whether the following statements are true and give an explanation or counterexample.
c. If the terms of the sequence {aₙ} are positive and increasing, then the sequence of partial sums for the series ∑⁽∞⁾ₖ₌₁ aₖ diverges.
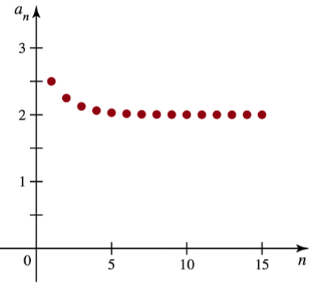
Problem 10.1.49
49–50. Limits from graphs Consider the following sequences. Find the first four terms of the sequence .Based on part (a) and the figure, determine a plausible limit of the sequence.
aₙ = 2 + 2⁻ⁿ ; n = 1, 2, 3, …
Problem 10.1.53
51–56. {Use of Tech} Recurrence relations Consider the following recurrence relations. Make a table with at least ten terms and determine a plausible limit of the sequence or state that the sequence diverges.
aₙ₊₁ = 4aₙ + 1 a₀ = 1
Problem 10.1.47
45–48. {Use of Tech} Explicit formulas for sequences Consider the formulas for the following sequences {aₙ}ₙ₌₁∞
Make a table with at least ten terms and determine a plausible limit of the sequence or state that the sequence diverges.
aₙ = ⁿ² + n ; n = 1, 2, 3, …