Back
Problem 5.3.100
Determine the intervals on which the function g(π) = β«ββ° t / (tΒ² + 1) dt is concave up or concave down.
Problem 5.3.5
The linear function Ζ(π) = 3 β π is decreasing on the interval [0, 3]. Is its area function for Ζ (with left endpoint 0) increasing or decreasing on the interval [0, 3]? Draw a picture and explain.
Problem 5.3.15a
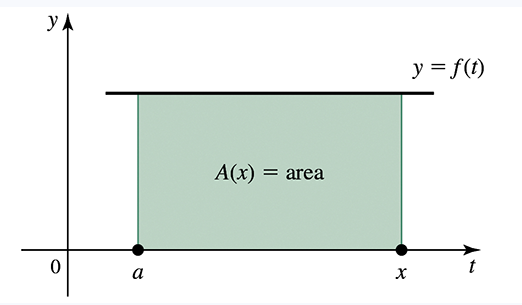
Area functions for constant functions Consider the following functions Ζ and real numbers a (see figure).
(a) Find and graph the area function A(π) = β«βΛ£ Ζ(t) dt for Ζ.
Ζ(t) = 5 , a = 0
Problem 5.3.16b
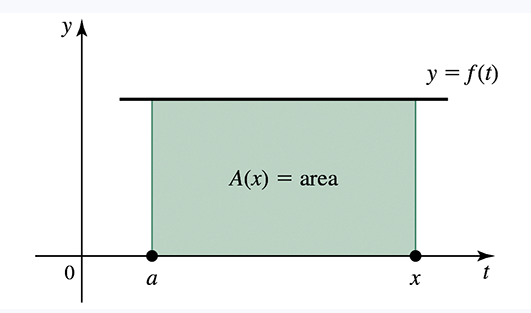
Area functions for constant functions Consider the following functions Ζ and real numbers a (see figure).
(b) Verify that .A'(π) = Ζ(π)
Ζ(t) = 5 , a = -5
Problem 5.3.20a
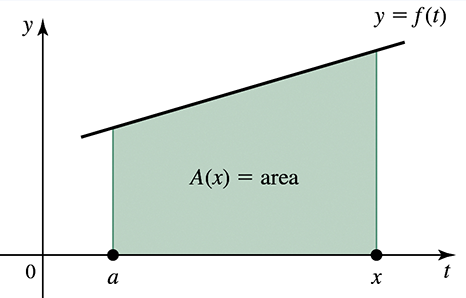
Area functions for linear functions Consider the following functions Ζ and real numbers a (see figure).
(a) Find and graph the area function A (π) = β«βΛ£ Ζ(t) dt .
Ζ(t) = 2t + 5 , a = 0
Problem 5.3.21b
Area functions for linear functions Consider the following functions Ζ and real numbers a (see figure).
(b) Verify that A'(π) = Ζ(π).
Ζ(t) = 3t + 1 , a = 2
Problem 5.3.22a
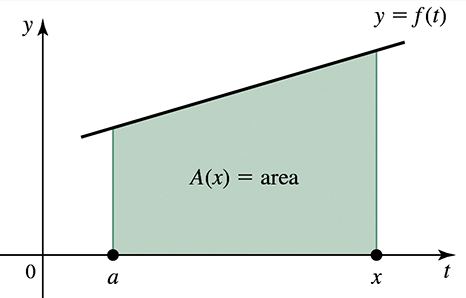
Area functions for linear functions Consider the following functions Ζ and real numbers a (see figure).
(a) Find and graph the area function A (π) = β«βΛ£ Ζ(t) dt .
<IMAGE>
Ζ(t) = 4t + 2 , a = 0
Problem 5.3.88b
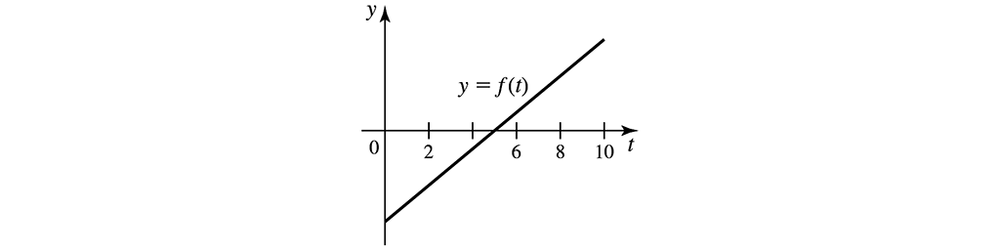
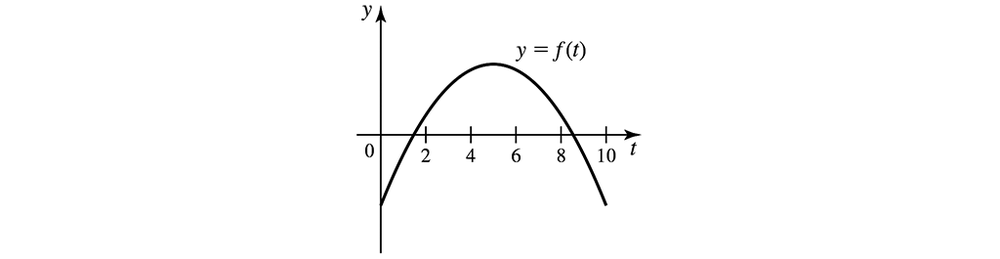
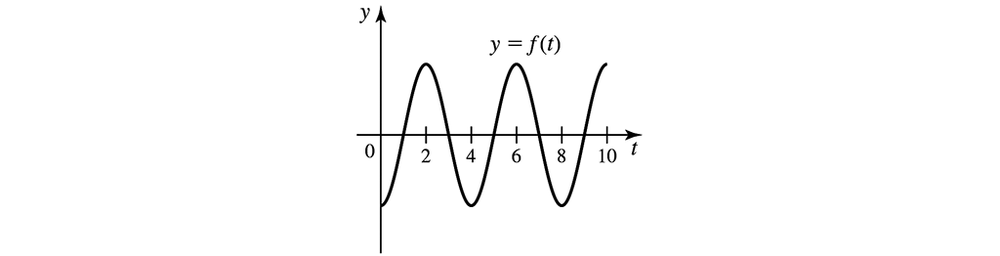
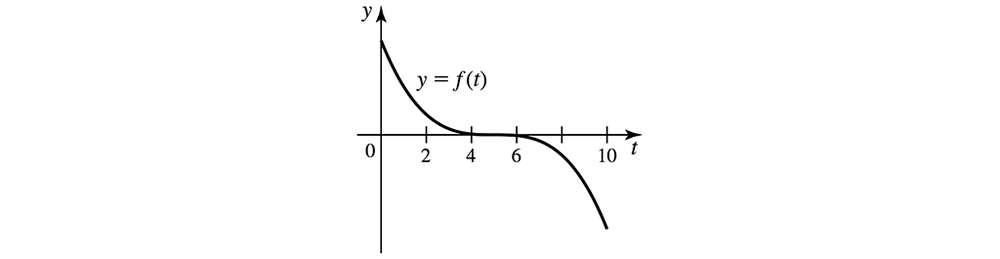
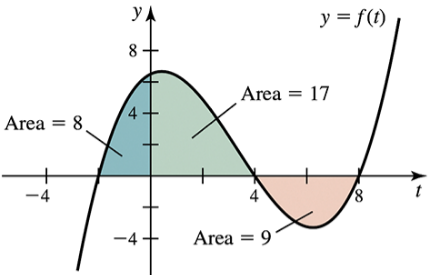
Working with area functions Consider the function Ζ and its graph.
(b) Estimate the points (if any) at which A has a local maximum or minimum.
Problem 5.3.89a
Working with area functions Consider the function Ζ and its graph.
(a) Estimate the zeros of the area function A(π) = β«βΛ£ Ζ(t) dt , for 0 β€ π β€ 10 .
Problem 5.3.90c
Working with area functions Consider the function Ζ and its graph.
(c) Sketch a graph of A, for 0 β€ π β€ 10 , without a scale on the y-axis.
Problem 5.3.91b
Working with area functions Consider the function Ζ and its graph.
(b) Estimate the points (if any) at which A has a local maximum or minimum.
Problem 5.3.93
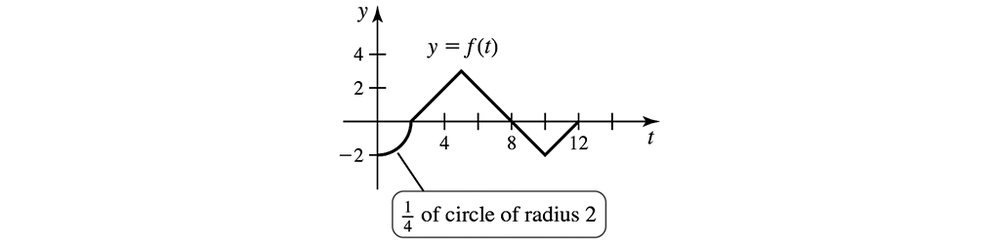
Area functions from graphs The graph of Ζ is given in the figure. A(π) = β«βΛ£ Ζ(t) dt and evaluate A(2), A(5), A(8), and A(12).ββ
Problem 5.3.22b
Area functions for linear functions Consider the following functions Ζ and real numbers a (see figure).
b) Verify that A'(π) = Ζ(π).
Ζ(t) = 4t + 2 , a = 0
Problem 5.3.23
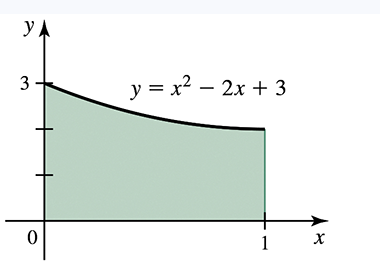
Definite integrals Evaluate the following integrals using the Fundamental Theorem of Calculus. Explain why your result is consistent with the figure.
β«βΒΉ (πΒ² β 2π + 3) dπ
Problem 5.3.102b
{Use of Tech} Functions defined by integrals Consider the function g, which is given in terms of a definite integral with a variable upper limit.
(b) Calculate g'(π)
g(π) = β«βΛ£ sin (ΟtΒ² ) dt ( a Fresnel integral)
Problem 5.3.17b
Area functions for the same linear function Let Ζ(t) = t and consider the two area functions A(π) = β«βΛ£ Ζ(t) dt and F(π) = β«βΛ£ Ζ(t) dt .
(b) Evaluate F(4) and F(6). Then use geometry to find an expression for F (π) , for π β₯ 2.
Problem 5.3.101b
{Use of Tech} Functions defined by integrals Consider the function g, which is given in terms of a definite integral with a variable upper limit.
b) Calculate g'(π)
g(π) = β«βΛ£ sinΒ² t dt
Problem 5.3.114
Max/min of area functions Suppose Ζ is continuous on [0 ,β) and A(π) is the net area of the region bounded by the graph of Ζ and the t-axis on [0, x]. Show that the local maxima and minima of A occur at the zeros of Ζ. Verify this fact with the function Ζ(π) = πΒ² - 10π.
Problem 5.3.108
Evaluate
lim [ β«βΛ£ β(tΒ² + t + 3dt) ] / (πΒ² β4)
πβ2
Problem 5.3.111a
Zero net area Consider the function Ζ(π) = πΒ² β 4π .
(a) Graph Ζ on the interval π β₯ 0.
Problem 5.3.18a
Area functions for the same linear function Let Ζ(t) = 2t β 2 and consider the two area functions A (π) = β«βΛ£ Ζ(t) dt and F(π) = β«βΛ£ Ζ(t) dt .
(a) Evaluate A (2) and A (3). Then use geometry to find an expression for A (π) , for π β₯ 1 .
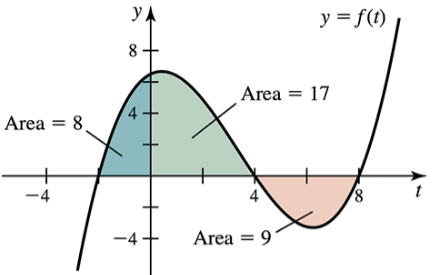
Problem 5.3.13a
Area functions The graph of Ζ is shown in the figure. Let A(x) = β«ββΛ£ Ζ(t) dt and F(x) = β«βΛ£ Ζ(t) dt be two area functions for Ζ. Evaluate the following area functions.
(a) A (β2)
Problem 5.3.13d
Area functions The graph of Ζ is shown in the figure. Let A(x) = β«ββΛ£ Ζ(t) dt and F(x) = β«βΛ£ Ζ(t) dt be two area functions for Ζ. Evaluate the following area functions.
(d) F(4)
Problem 5.3.27
Definite integrals Evaluate the following integrals using the Fundamental Theorem of Calculus. Sketch the graph of the integrand and shade the region whose net area you have found.
β«ββ΅ (πΒ²β9) dπ
Problem 5.3.103
{Use of Tech} Areas of regions Find the area of the region π bounded by the graph of Ζ and the π-axis on the given interval. Graph Ζ and show the region π .
Ζ(π) = 2 β |π| on [ β 2 , 4]
Problem 5.3.106
{Use of Tech} Areas of regions Find the area of the region π bounded by the graph of Ζ and the π-axis on the given interval. Graph Ζ and show the region π .
Ζ(π) = πΒ² (π β 2) on [ β1 , 3]
Problem 5.3.107b
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(b) Suppose Ζ is a negative increasing function, for π > 0 . Then the area function A(π) = β«βΛ£ Ζ(t) dt is a decreasing function of π .
Problem 5.3.107c
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(c) The functions p(π) = sin 3π and q(π) = 4 sin 3π are antiderivatives of the same function.
Problem 5.3.107d
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
(d) If A(π) = 3πΒ²β πβ 3 is an area function for Ζ, then
B(π) = 3πΒ² β π is also an area function for Ζ.
Problem 5.3.111c
Zero net area Consider the function Ζ(π) = πΒ² β 4π .
c) In general, for the function Ζ(π) = πΒ² β aπ, where a > 0, for what value of b > 0 (as a function of a) is β«βα΅ Ζ(π) dπ = 0 ?
