Back
Problem 5.3.112
Cubic zero net area Consider the graph of the cubic y = π (πβ a) (πβ b), where 0 < a < b. Verify that the graph bounds a region above the π-axis, for 0 < π < a , and bounds a region below the π-axis, for a < π < b. What is the relationship between a and b if the areas of these two regions are equal?
Problem 5.4.25
Average values Find the average value of the following functions on the given interval. Draw a graph of the function and indicate the average value.
Ζ(π) = πΒ³ on [β1, 1]
Problem 5.4.27
Average values Find the average value of the following functions on the given interval. Draw a graph of the function and indicate the average value.
Ζ(π) = 1/(πΒ² + 1) on [β1, 1]
Problem 5.4.29
Average values Find the average value of the following functions on the given interval. Draw a graph of the function and indicate the average value.
Ζ(π) = cos π on [βΟ/2 , Ο/2]
Problem 5.4.31
Average values Find the average value of the following functions on the given interval. Draw a graph of the function and indicate the average value.
Ζ(π) = πβΏ on [0,1] , for any positive integer n
Problem 5.4.33
Average distance on a parabola What is the average distance between the parabola y = 30π (20 β π ) and the π-axis on the interval [0, 20] ?
Problem 5.4.35
Average velocity The velocity in m/s of an object moving along a line over the time interval [0,6] is v (t) = tΒ² + 3t. Find the average velocity of the object over this time interval.
Problem 5.4.38
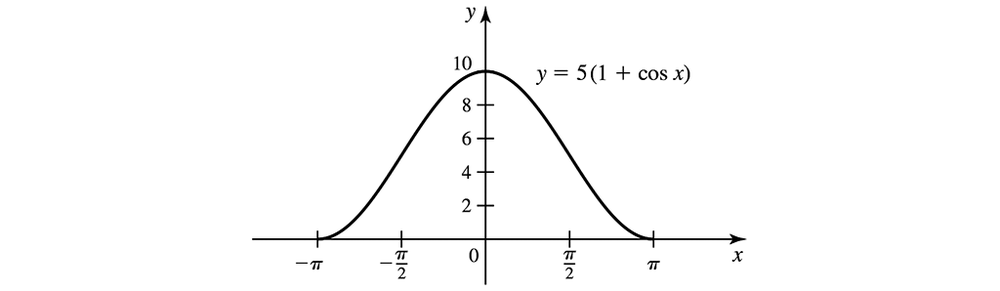
Average height of a wave The surface of a water wave is described by y = 5 (1 + cos π) , for β Ο β€ π β€ Ο, where y = 0 corresponds to a trough of the wave (see figure). Find the average height of the wave above the trough on [ βΟ , Ο] .
Problem 5.4.39
Mean Value Theorem for Integrals Find or approximate all points at which the given function equals its average value on the given interval.
Ζ(π) = 8 β 2π on [0, 4]
Problem 5.4.43
Mean Value Theorem for Integrals Find or approximate all points at which the given function equals its average value on the given interval.
Ζ(π) = 1 β |π| on [β1, 1]
Problem 5.4.47
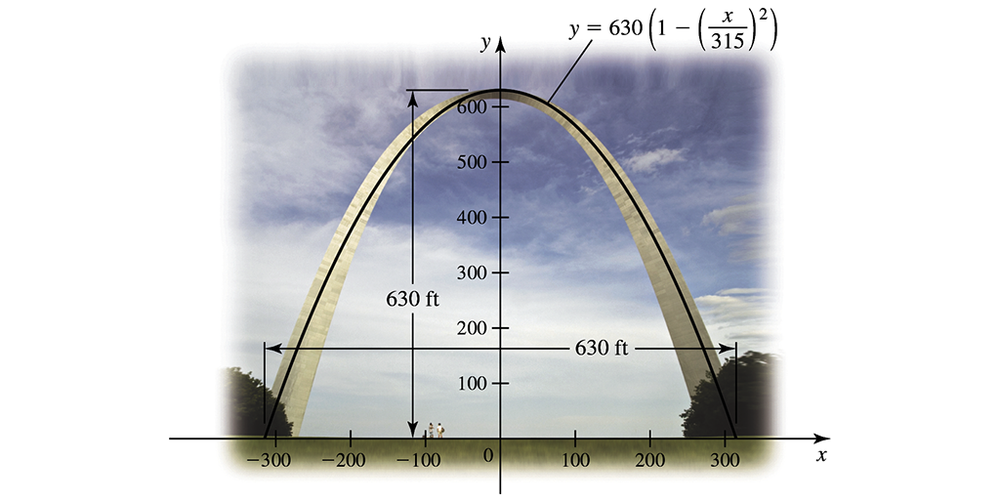
Gateway Arch The Gateway Arch in St. Louis is 630 ft high and has a 630-ft base. Its shape can be modeled by the parabola y = 630 (1β (π/315)Β²) . Find the average height of the arch above the ground.
Problem 5.4.49
Symmetry of composite functions Prove that the integrand is either even or odd. Then give the value of the integral or show how it can be simplified. Assume f and g are even functions and p and q are odd functions.
β«α΅ββ Ζ(g(π)) dπ
Problem 5.4.45a
Explain why or why notββ Determine whether the following statements are true and give an explanation or counterexample.
(a) If Ζ is symmetric about the line π = 2 , then β«ββ΄ Ζ(π) dπ = 2 β«βΒ² Ζ(π) dπ.
Problem 5.4.46a
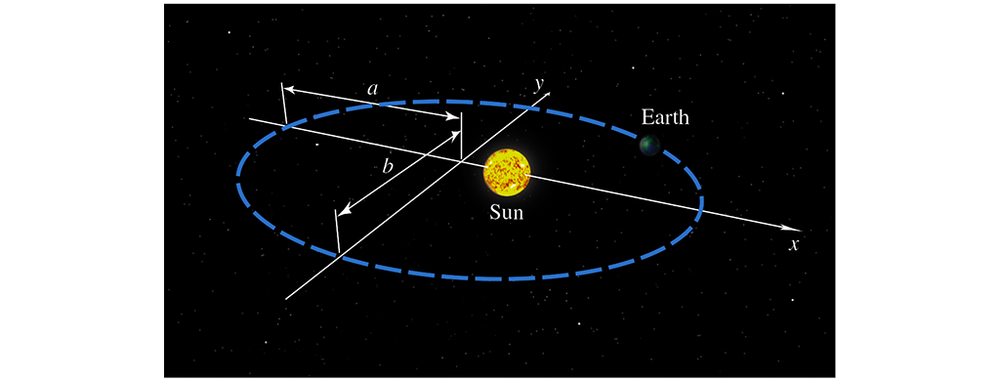
Planetary orbits The planets orbit the Sun in elliptical orbits with the Sun at one focus (see Section 12.4 for more on ellipses). The equation of an ellipse whose dimensions are 2a in the π-direction and 2b in the y-direction is (πΒ²/aΒ²) + (yΒ² /bΒ²) = 1.
(a) Let dΒ² denote the square of the distance from a planet to the center of the ellipse at (0, 0). Integrate over the interval [ βa, a] to show that the average value of dΒ² is (aΒ² + 2bΒ²) /3 .
Problem 5.4.50
Symmetry of composite functions Prove that the integrand is either even or odd. Then give the value of the integral or show how it can be simplified. Assume f and g are even functions and p and q are odd functions.
β«α΅ββ Ζ(p(π)) dπ
Problem 5.4.53a
Average value with a parameter Consider the function Ζ(π) = aπ (1βπ) on the interval [0, 1], where a is a positive real number.
(a) Find the average value of Ζ as a function of a .
Problem 5.4.4a
Suppose Ζ is an odd function, β«ββ΄ Ζ(π) dπ = 3 , and β«ββΈ Ζ(π) dπ = 9 .
(a) Evaluate β«βββ΄ Ζ(π) dπ .
Problem 5.4.3b
Suppose Ζ is an even function and β«βΈββ Ζ(π) dπ = 18
(b) Evaluate β«βββΈ πΖ(π) dπ .
Problem 5.4.1
If Ζ is an odd function, why is β«α΅ββ Ζ(π) dπ = 0?
Problem 5.4.45c
Explain why or why notββ Determine whether the following statements are true and give an explanation or counterexample.
(c) The average value of a linear function on an interval [a, b] is the function value at the midpoint of [a, b] .
Problem 5.4.5
Use symmetry to explain why.
β«β΄ββ (5πβ΄ + 3πΒ³ + 2πΒ² + π + 1) dπ = 2 β«ββ΄ (5πβ΄ + 2πΒ² + π + 1) dπ .
Problem 5.4.7
Is xΒΉΒ² an even or odd function? Is sin xΒ² an even or odd function?
Problem 5.4.9
Explain the statement that a continuous function on an interval [a,b] equals its average value at some point on (a,b).
Problem 5.4.12
Symmetry in integrals Use symmetry to evaluate the following integrals.
β«Β²β°β°ββββ 2xβ΅ dx
Problem 5.4.15
Symmetry in integrals Use symmetry to evaluate the following integrals.
β«Β²ββ (xΒ² + xΒ³) dx
Problem 5.4.18
Symmetry in integrals Use symmetry to evaluate the following integrals.
β«βΟ/β^Ο/Β² 5 sin ΞΈ dΞΈ
Problem 5.4.21
Symmetry in integrals Use symmetry to evaluate the following integrals.
β«βΟ/β^Ο/β΄ secΒ² x dx
Problem 5.4.23
Symmetry in integrals Use symmetry to evaluate the following integrals.
β«Β²ββ [(xΒ³ β 4x) / (xΒ² + 1)] dx
Problem 5.4.56
Average value of the derivative Suppose Ζ ' is a continuous function for all real numbers. Show that the average value of the derivative on an interval [a, b] is Ζβ»' = (Ζ(b) βΖ(a))/ (bβa) . Interpret this result in terms of secant lines.
Problem 5.4.59b
Generalizing the Mean Value Theorem for Integrals Suppose Ζ and g are continuous on [a, b] and let h(π) = (πβb) β«βΛ£ Ζ(t) dt + (πβa) β«βα΅g(t)dt.
(b) Show that there is a number c in (a, b) such that β«βαΆ Ζ(t) dt = Ζ(c) (b β c)
(Source: The College Mathematics Journal, 33, 5, Nov 2002)
