Back
BackProblem 6.3.12
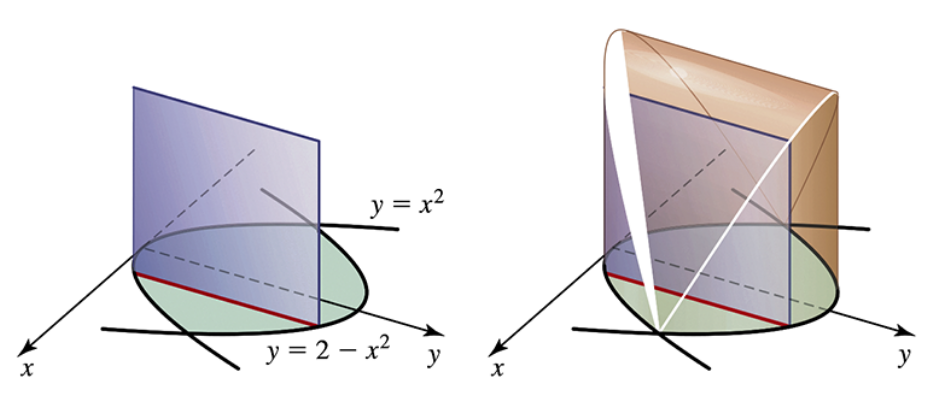
Use the general slicing method to find the volume of the following solids.
The solid whose base is the region bounded by the curves y=x^2 and y=2−x^2, and whose cross sections through the solid perpendicular to the x-axis are squares
Problem 6.3.61a
"Determine whether the following statements are true and give an explanation or counterexample.
a. A pyramid is a solid of revolution. "
Problem 6.3.61b
"Determine whether the following statements are true and give an explanation or counterexample.
b. The volume of a hemisphere can be computed using the disk method. "
Problem 6.3.15
Use the general slicing method to find the volume of the following solids.
The solid whose base is the triangle with vertices (0, 0), (2, 0), and (0, 2), and whose cross sections perpendicular to the base and parallel to the y-axis are semicircles
Problem 6.3.62
Use calculus to find the volume of a tetrahedron (pyramid with four triangular faces), all of whose edges have length 4.
Problem 6.3.64
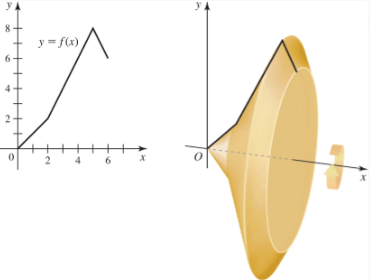
Let f(x) = {x if 0≤x≤2
2x−2 if 2<x≤5
−2x+18 if 5<x≤6.
Find the volume of the solid formed when the region bounded by the graph of f, the x-axis, and the line x=6 is revolved about the x-axis.
Problem 6.3.67
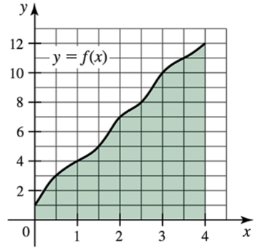
Suppose the region bounded by the curve y=f(x) from x=0 to x=4 (see figure) is revolved about the x-axis to form a solid of revolution. Use left, right, and midpoint Riemann sums, with n=4 subintervals of equal length, to estimate the volume of the solid of revolution.
Problem 6.3.40
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=x^2,y=2−x, and y=0; about the y-axis
Problem 6.3.17
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=2x,y=0 , and x=3; about the x-axis (Verify that your answer agrees with the volume formula for a cone.)
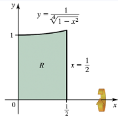
Problem 6.3.20
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=1 / 4√1 − x^2,y=0,x=0, and x=12; about the x-axis
Problem 6.3.22
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=0,y=lnx,y=2, and x=0; about the y-axis
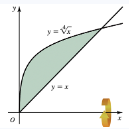
Problem 6.3.24
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=x and y=4√x; about the x-axis
Problem 6.3.26
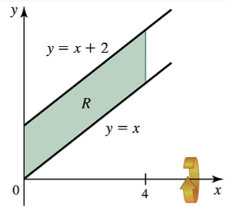
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=x,y=x+2,x=0, and x=4 ; about the x-axis
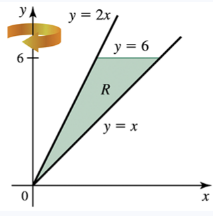
Problem 6.3.28
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=x,y=2x, and y=6 ; about the y-axis
Problem 6.3.31
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=sin xon [0,π] and y=0 ; about the x-axis (Hint: Recall that sin^2 x=1 − cos2x / 2.
Problem 6.3.34
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=√sin x,y=1, and x=0; about the x-axis
Problem 6.3.36
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=|x| and y=2−x^2; about the x-axis
Problem 6.3.43
Let R be the region bounded by the following curves. Find the volume of the solid generated when R is revolved about the given axis.
y=ln x,y=ln x^2; and y=ln 8; about the y-axis
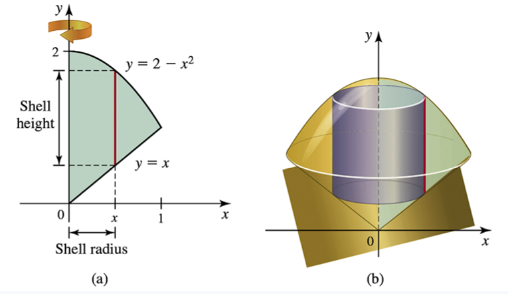
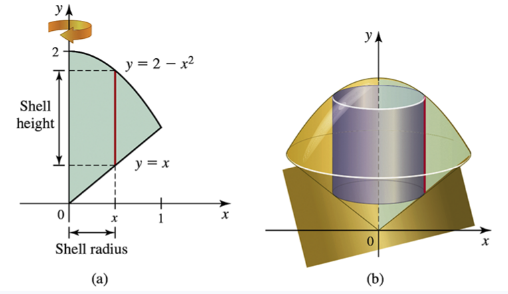
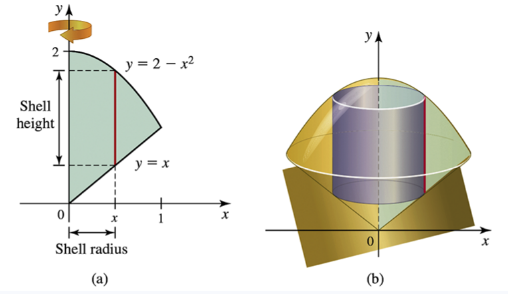
Problem 6.4.5a
Let R be the region in the first quadrant bounded above by the curve y=2−x² and bounded below by the line y=x. Suppose the shell method is used to determine the volume of the solid generated by revolving R about the y-axis.
a. What is the radius of a cylindrical shell at a point x in [0, 2]?
Problem 6.4.5b
Let R be the region in the first quadrant bounded above by the curve y=2−x² and bounded below by the line y=x. Suppose the shell method is used to determine the volume of the solid generated by revolving R about the y-axis.
b. What is the height of a cylindrical shell at a point x in [0, 2]?
Problem 6.4.5c
Let R be the region in the first quadrant bounded above by the curve y=2−x² and bounded below by the line y=x. Suppose the shell method is used to determine the volume of the solid generated by revolving R about the y-axis.
c. Write an integral for the volume of the solid using the shell method.
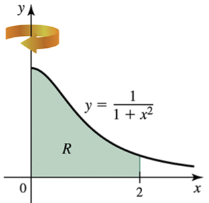
Problem 6.4.10
9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis.
y = (1+x²)^−1,y = 0,x = 0, and x = 2; about the y-axis
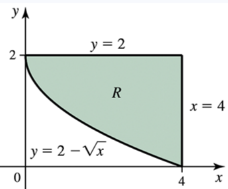
Problem 6.4.8a
6–8. Let R be the region bounded by the curves y = 2−√x,y=2, and x=4 in the first quadrant.
Suppose the shell method is used to determine the volume of the solid generated by revolving R about the line x=4.
a. What is the radius of a cylindrical shell at a point x in [0, 4]?
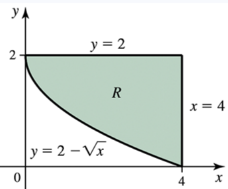
Problem 6.4.8b
6–8. Let R be the region bounded by the curves y = 2−√x,y=2, and x=4 in the first quadrant.
Suppose the shell method is used to determine the volume of the solid generated by revolving R about the line x=4.
b. What is the height of a cylindrical shell at a point x in [0, 4]?
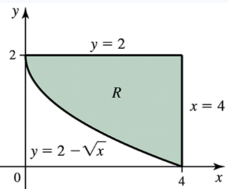
Problem 6.4.8c
6–8. Let R be the region bounded by the curves y = 2−√x,y=2, and x=4 in the first quadrant.
Suppose the shell method is used to determine the volume of the solid generated by revolving R about the line x=4.
c. Write an integral for the volume of the solid using the shell method.
Problem 6.4.1
Assume f and g are continuous, with f(x) ≥ g(x) ≥ 0 on [a, b]. The region bounded by the graphs of f and g and the lines x=a and x=b is revolved about the y-axis. Write the integral given by the shell method that equals the volume of the resulting solid.
Problem 6.4.4
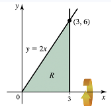
Look again at the region R in Figure 6.38 (p. 439). Explain why it would be difficult to use the washer method to find the volume of the solid of revolution that results when R is revolved about the y-axis.
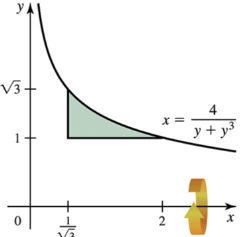
Problem 6.4.16
9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis.
x = 4 / y + y³,x = 1/√3, and y=1; about the x-axis
Problem 6.4.19
9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis.
y = 1−x²,x = 0, and y = 0, in the first quadrant; about the y-axis
Problem 6.4.13
9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis.
y = √x,y=0, and x=4; about the x-axis