Back
BackProblem 12.2.56
53–56. Simple curves Tabulate and plot enough points to sketch a graph of the following equations.
r = 1 - cos θ
Problem 12.2.58
57–64. Graphing polar curves Graph the following equations. Use a graphing utility to check your work and produce a final graph.
r = 2 - 2 sin θ b
Problem 12.2.60
57–64. Graphing polar curves Graph the following equations. Use a graphing utility to check your work and produce a final graph.
r² = 4 sin θ
Problem 12.2.63
57–64. Graphing polar curves Graph the following equations. Use a graphing utility to check your work and produce a final graph.
r = sin 3θ
Problem 12.2.111
Cartesian lemniscate Find the equation in Cartesian coordinates of the lemniscate r² = a² cos 2θ, where a is a real number.
Problem 12.2.109
Subtle symmetry Without using a graphing utility, determine the symmetries (if any) of the curve r=4-sin (θ/2)
Problem 12.2.108a
Channel flow Water flows in a shallow semicircular channel with inner and outer radii of 1 m and 2 m (see figure). At a point P(r,θ) in the channel, the flow is in the tangential direction (counterclock wise along circles), and it depends only on r, the distance from the center of the semicircles.
a. Express the region formed by the channel as a set in polar coordinates.
Problem 12.2.106d
(Use of Tech) Finger curves: r = f(θ) = cos(aᶿ) - 1.5, where a = (1 + 12π)^(1/(2π)) ≈ 1.78933
d. Plot the curve with various values of k. How many fingers can you produce?
Problem 12.2.4
What is the polar equation of a circle of radius √(a²+b²) centered at (a, b)?
Problem 12.2.5
What is the polar equation of the vertical line x = 5?
Problem 12.2.85a
Navigating A plane is 150 miles north of a radar station, and 30 minutes later it is 60 degree east of north at a distance of 100 miles from the radar station. Assume the plane flies on a straight line and maintains constant altitude during this 30-minute period.
a. Find the distance traveled during this 30-minute period.
Problem 12.2.106a
(Use of Tech) Finger curves: r = f(θ) = cos(aᶿ) - 1.5, where a = (1 + 12π)^(1/(2π)) ≈ 1.78933
a. Show that f(0) = f(2π) and find the point on the curve that corresponds to θ = 0 and θ = 2π.
Problem 12.2.102
102–104. Spirals Graph the following spirals. Indicate the direction in which the spiral is generated as θ increases, where θ>0. Let a=1 and a=−1.
Spiral of Archimedes: r = aθ
Problem 12.2.82
80–83. Equations of circles Use the results of Exercises 78–79 to describe and graph the following circles.
r² - 8r cos(θ - π/2) = 9
Problem 12.2.77d
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
d. The point (3,π/2) lies on the graph of r=3 cos 2θ.
Problem 12.2.77a
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
a. The point with Cartesian coordinates (−2, 2) has polar coordinates (2√2, 3π/4), (2√2, 11π/4), (2√2, −5π/4), and (−2√2,−π/4).
Problem 12.3.87
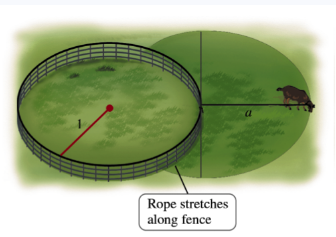
85–87. Grazing goat problems Consider the following sequence of problems related to grazing goats tied to a rope. (See the Guided Project Grazing goat problems.)
A circular corral of unit radius is enclosed by a fence. A goat is outside the corral and tied to the fence with a rope of length 0≤a ≤ π (see figure). What is the area of the region (outside the corral) that the goat can reach?
Problem 12.3.5
What is the slope of the line θ=π/3?
Problem 12.3.8
Without calculating derivatives, determine the slopes of each of the lines tangent to the curve r=8 cos θ−4 at the origin.
Problem 12.3.11
11–20. Slopes of tangent lines Find the slope of the line tangent to the following polar curves at the given points.
r = 1 - sin θ; (1/2, π/6)
Problem 12.3.14
11–20. Slopes of tangent lines Find the slope of the line tangent to the following polar curves at the given points.
r = 4 + sin θ; (4, 0) and (3, 3π/2)
Problem 12.3.17
11–20. Slopes of tangent lines Find the slope of the line tangent to the following polar curves at the given points.
r = 4 cos 2θ; at the tips of the leaves
Problem 12.3.20
11–20. Slopes of tangent lines Find the slope of the line tangent to the following polar curves at the given points.
r = 2θ; (π/2, π/4)
Problem 12.3.22
Tangent line at the origin Find the polar equation of the line tangent to the polar curve r=4cosθ at the origin. Explain why the slope of this line is undefined.
Problem 12.3.25
25–28. Horizontal and vertical tangents Find the points at which the following polar curves have horizontal or vertical tangent lines.
r = 4 cos θ
Problem 12.3.29
29–32. Intersection points Use algebraic methods to find as many intersection points of the following curves as possible. Use graphical methods to identify the remaining intersection points.
r = 2 cos θ and r = 1 + cos θ
Problem 12.3.31
29–32. Intersection points Use algebraic methods to find as many intersection points of the following curves as possible. Use graphical methods to identify the remaining intersection points.
r = 1 and r = 2 sin 2θ
Problem 12.3.33
33–40. Areas of regions Make a sketch of the region and its bounding curves. Find the area of the region.
The region inside the curve r = √(cos θ)
Problem 12.3.35
33–40. Areas of regions Make a sketch of the region and its bounding curves. Find the area of the region.
The region inside the circle r = 8 sin θ
Problem 12.3.37
33–40. Areas of regions Make a sketch of the region and its bounding curves. Find the area of the region.
The region inside the limaçon r = 2 + cos θ