Back
BackProblem 12.1.89c
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
c. The parametric equations x=t, y=t², for t≥0, describe the complete parabola y=x².
Problem 12.1.89e
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
e. There are two points on the curve x=−4 cos t, y=sin t, for 0≤t≤2π, at which there is a vertical tangent line.
Problem 12.1.105
Find the area of the region bounded by the astroid x = cos³ t, y = sin³ t, for 0 ≤ t ≤ 2π
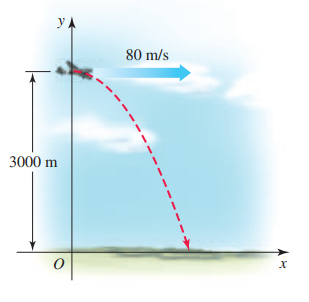
Problem 12.1.64
Air drop A plane traveling horizontally at 80 m/s over flat ground at an elevation of 3000 m releases an emergency packet. The trajectory of the packet is given by
x = 80t, y = −4.9t² + 3000, t ≥ 0
where the origin is the point on the ground directly beneath the plane at the moment of the release (see figure). Graph the trajectory of the packet and find the coordinates of the point where the packet lands.
Problem 12.1.65
Air drop—inverse problem A plane traveling horizontally at 100 m/s over flat ground at an elevation of 4000 m must drop an emergency packet on a target on the ground. The trajectory of the packet is given by
x = 100t, y = −4.9t² + 4000, t ≥ 0
where the origin is the point on the ground directly beneath the plane at the moment of the release. How many horizontal meters before the target should the packet be released in order to hit the target?
Problem 12.1.114
Second derivative Assume a curve is given by the parametric equations x=f(t) and y=g(t), where f and g are twice differentiable. Use the Chain Rule to show that y″x=(fʹ(t)g″(t) − gʹ(t)f″(t))/(fʹ(t))³.
Problem 12.1.63
{Use of Tech} Implicit function graph Explain and carry out a method for graphing the curve x = 1 + cos² y − sin² y using parametric equations and a graphing utility.
Problem 12.2.52
49–52. Cartesian-to-polar coordinates Convert the following equations to polar coordinates.
(x - 1)² + y² = 1
Problem 12.2.50
49–52. Cartesian-to-polar coordinates Convert the following equations to polar coordinates.
y = 3
Problem 12.2.49
49–52. Cartesian-to-polar coordinates Convert the following equations to polar coordinates.
y = x²
Problem 12.2.46
37–48. Polar-to-Cartesian coordinates Convert the following equations to Cartesian coordinates. Describe the resulting curve.
r = sin θ sec² θ
Problem 12.2.43
37–48. Polar-to-Cartesian coordinates Convert the following equations to Cartesian coordinates. Describe the resulting curve.
r = 6 cos θ + 8 sin θ
Problem 12.2.40
37–48. Polar-to-Cartesian coordinates Convert the following equations to Cartesian coordinates. Describe the resulting curve.
r = 3 csc θ
Problem 12.2.37
37–48. Polar-to-Cartesian coordinates Convert the following equations to Cartesian coordinates. Describe the resulting curve.
r cos θ = -4
Problem 12.2.35
31–36. Converting coordinates Express the following Cartesian coordinates in polar coordinates in at least two different ways.
(-4, 4√3)
Problem 12.2.33
31–36. Converting coordinates Express the following Cartesian coordinates in polar coordinates in at least two different ways.
(1, √3)
Problem 12.2.30
25–30. Converting coordinates Express the following polar coordinates in Cartesian coordinates.
(4, 5π)
Problem 12.2.28
25–30. Converting coordinates Express the following polar coordinates in Cartesian coordinates.
(2, 7π/4)
Problem 12.2.26
25–30. Converting coordinates Express the following polar coordinates in Cartesian coordinates.
(1, 2π/3)
Problem 12.2.1
Plot the points with polar coordinates (2, π/6) and (−3, −π/2). Give two alternative sets of coordinate pairs for both points.
Problem 12.2.2
Write the equations that are used to express a point with polar coordinates (r, θ) in Cartesian coordinates.
Problem 12.2.6
What is the polar equation of the horizontal line y = 5?
Problem 12.2.8
Given three polar coordinate representations for the origin.
Problem 12.2.11
9–13. Graph the points with the following polar coordinates. Give two alternative representations of the points in polar coordinates.
(-1, -π/3)
Problem 12.2.13
9–13. Graph the points with the following polar coordinates. Give two alternative representations of the points in polar coordinates.
(-4, 3π/2)
Problem 12.2.79
Circles in general Show that the polar equation
r² - 2r r₀ cos(θ - θ₀) = R² - r₀²
describes a circle of radius R whose center has polar coordinates (r₀, θ₀)
Problem 12.2.16
15–22. Sets in polar coordinates Sketch the following sets of points.
r = 3
Problem 12.2.18
15–22. Sets in polar coordinates Sketch the following sets of points.
2 ≤ r ≤ 8
Problem 12.2.20
15–22. Sets in polar coordinates Sketch the following sets of points.
1 < r < 2 and π/6 ≤ θ ≤ π/3
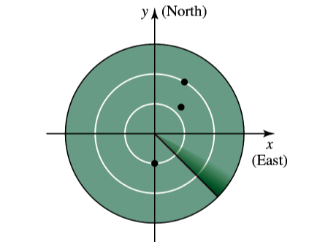
Problem 12.2.24
23–24. Radar Airplanes are equipped with transponders that allow air traffic controllers to see their locations on radar screens. Radar gives the distance of the plane from the radar station (located at the origin) and the angular position of the plane, typically measured in degrees clockwise from north.
A plane is 50 miles from a radar station at an angle of 10 dgeree clockwise from north. Find polar coordinates for the location of the plane.