Back
BackProblem 5.R.105c
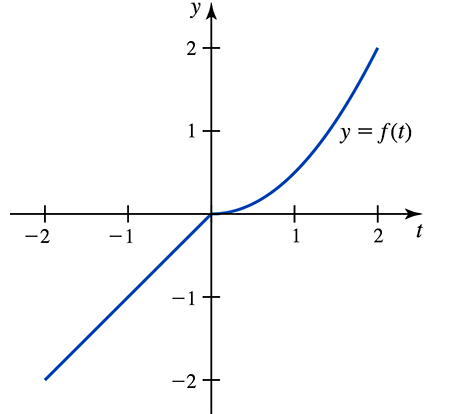
Area functions and the Fundamental Theorem Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.
(c) Use the Fundamental Theorem to find an expression for F '(𝓍) for 0 ≤ 𝓍 < 2.
Problem 5.R.105d
Area functions and the Fundamental Theorem Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.
(d) Evaluate F ' (―1) and F ' (1). Interpret these values.
Problem 5.R.105e
Area functions and the Fundamental Theorem Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.
(e) Evaluate F ''(―1) and F ''(1). Interpret these values.
Problem 5.R.105f
Consider the function
ƒ(t) = { t if ―2 ≤ t < 0
t²/2 if 0 ≤ t ≤ 2
and its graph shown below. Let F(𝓍) = ∫₋₁ˣ ƒ(t) dt and G(𝓍) = ∫₋₂ˣ ƒ(t) dt.
(f) Find a constant C such that F(𝓍) = G(𝓍) + C .
Problem 5.R.9a
Integration by Riemann sums Consider the integral ∫₁⁴ (3𝓍― 2) d𝓍.
(a) Evaluate the right Riemann sum for the integral with n = 3 .
Problem 5.R.9b
Integration by Riemann sums Consider the integral ∫₁⁴ (3𝓍― 2) d𝓍.
(b) Use summation notation to express the right Riemann sum in terms of a positive integer n .
Problem 5.R.9c
Integration by Riemann sums Consider the integral ∫₁⁴ (3𝓍― 2) d𝓍.
(c) Evaluate the definite integral by taking the limit as n →∞ of the Riemann sum in part (b).
Problem 5.R.9d
Integration by Riemann sums Consider the integral ∫₁⁴ (3𝓍― 2) d𝓍.
(a) Evaluate the right Riemann sum for the integral with n = 3 .
Problem 5.R.11
Limit definition of the definite integral Use the limit definition of the definite integral with right Riemann sums and a regular partition to evaluate the following definite integrals. Use the Fundamental Theorem of Calculus to check your answer.
∫₀² (𝓍²―4) d𝓍
Problem 5.R.13
Limit definition of the definite integral Use the limit definition of the definite integral with right Riemann sums and a regular partition to evaluate the following definite integrals. Use the Fundamental Theorem of Calculus to check your answer.
∫₀⁴ (𝓍³―𝓍) d𝓍
Problem 5.R.5
Estimate ∫₁⁴ √(4𝓍 + 1) d𝓍 by evaluating the left, right, and midpoint Riemann sums using a regular partition with n = 6 subintervals.
Problem 5.R.18
Properties of integrals Suppose ∫₁⁴ ƒ(𝓍) d𝓍 = 6 , ∫₁⁴ g(𝓍) d𝓍 = 4 and ∫₃⁴ ƒ(𝓍) d𝓍 = 2 . Evaluate the following integrals or state that there is not enough information.
―∫₄¹ 2ƒ(𝓍) d𝓍
Problem 5.R.21
Properties of integrals Suppose ∫₁⁴ ƒ(𝓍) d𝓍 = 6 , ∫₁⁴ g(𝓍) d𝓍 = 4 and ∫₃⁴ ƒ(𝓍) d𝓍 = 2 . Evaluate the following integrals or state that there is not enough information.
∫₁³ ƒ(𝓍)/g(𝓍) d𝓍
Problem 5.R.30
Evaluate the following derivatives.
d/d𝓍 ∫₃ᵉˣ cos t² dt
Problem 5.R.35
Find the intervals on which ƒ(𝓍) = ∫ₓ¹ (t―3) (t―6)¹¹ dt is increasing and the intervals on which it is decreasing.
Problem 5.R.39
Evaluating integrals Evaluate the following integrals.
∫₋₂² (3𝓍⁴―2𝓍 + 1) d𝓍
Problem 5.R.43
Evaluating integrals Evaluate the following integrals.
∫₀¹ √𝓍 (√𝓍 + 1) d𝓍
Problem 5.R.45
Evaluating integrals Evaluate the following integrals.
∫π/₆^π/³ (sec² t + csc² t) dt
Problem 5.R.46
Evaluating integrals Evaluate the following integrals.
∫π/₁₂^π/⁹ (csc 3𝓍 cot 3𝓍 + sec 3𝓍 tan 3𝓍) d𝓍
Problem 5.R.48
Evaluating integrals Evaluate the following integrals.
∫₁⁴ ((√v + v) / v ) dv
Problem 5.R.50
Evaluating integrals Evaluate the following integrals.
∫₁ᵉ d𝓍 / [𝓍(1 + ln 𝓍)]
Problem 5.R.55
Evaluating integrals Evaluate the following integrals.
∫₀¹ 𝓍 • 2ˣ²⁺¹ d𝓍
Problem 5.R.57
Evaluating integrals Evaluate the following integrals.
∫₀² (2𝓍 + 1)³ d𝓍
Problem 5.R.65
Evaluating integrals Evaluate the following integrals.
∫₀^²π cos² 𝓍/6 d𝓍
Problem 5.R.71
Evaluating integrals Evaluate the following integrals.
∫₋₅⁵ ω³ /√(ω⁵⁰ + ω²⁰ + 1) dω (Hint: Use symmetry . )
Problem 5.R.81
Evaluating integrals Evaluate the following integrals.
∫√₂/₅^²/⁵ d𝓍/𝓍√(25𝓍² ―1)
Problem 5.R.84
Evaluating integrals Evaluate the following integrals.
∫₋π/₂^π/² (cos 2𝓍 + cos 𝓍 sin 𝓍 ― 3 sin 𝓍⁵) d𝓍
Problem 5.R.86
Evaluating integrals Evaluate the following integrals.
∫₀⁵ |2𝓍―8|d𝓍
Problem 5.R.95
Displacement from velocity A particle moves along a line with a velocity given by v(t) = 5 sin πt, starting with an initial position s(0) = 0 . Find the displacement of the particle between t = 0 and t = 2 , which is given by s(t) = ∫₀² v(t) dt . Find the distance traveled by the particle during this interval, which is ∫₀² |v(t)| dt .
Problem 5.R.96a
Velocity to displacement An object travels on the 𝓍-axis with a velocity given by v(t) = 2t + 5, for 0 ≤ t ≤ 4.
(a) How far does the object travel, for 0 ≤ t ≤ 4 ?