Explain the steps required to find the length of a curve x = g(y) between y=c and y=d.

Equal integrals Without evaluating integrals, explain the following equalities. (Hint: Draw pictures.)

b. ∫²₀(25−(x²+1)²) dx = 2∫₁⁵ y√y−1 dy

Volumes without calculus Solve the following problems with and without calculus. A good picture helps.

b. A cube is inscribed in a right circular cone with a radius of 1 and a height of 3. What is the volume of the cube?

Different axes of revolution Suppose R is the region bounded by y=f(x) and y=g(x) on the interval [a, b], where f(x)≥g(x).

b. How is this formula changed if x0>b?​​

64–68. Shell method Use the shell method to find the volume of the following solids.

A hole of radius r≤R is drilled symmetrically along the axis of a bullet. The bullet is formed by revolving the parabola y = 6(1−x²/R²) about the y-axis, where 0≤x≤R.​​

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

x = x³ ,y = 1, and x = 0; about the x-axis

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

{Use of Tech} y = 1 / (x² + 1)²,y=0,x=1, and x=2; about the y-axis​​

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

{Use of Tech} y = √sin^−1x,y = √π/2, and x=0; about the x-axis​​

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

{Use of Tech} y = In x/x²,y = 0,x = 3, about the y-axis​​

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

{Use of Tech} y = √50 -2x², in the first quadrant; about the x-axis

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

y = x³−x⁸+1,y=1; about the y-axis​​

9-34. Shell method Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about indicated axis. 

{Use of Tech} y² = ln x,y² = ln x³, and y=2; about the x-axis​​

35–38. Shell and washer methods Let R be the region bounded by the following curves. Use both the shell method and the washer method to find the volume of the solid generated when R is revolved about the indicated axis.

y = 8,y = 2x+2,x = 0, and x=2; about the y-axis

35–38. Shell and washer methods Let R be the region bounded by the following curves. Use both the shell method and the washer method to find the volume of the solid generated when R is revolved about the indicated axis.

y = (x−2)³ −2,x=0, and y=25; about the y-axis

39–44. Shell method about other lines Let R be the region bounded by y = x²,x=1, and y=0. Use the shell method to find the volume of the solid generated when R is revolved about the following lines.

x =2

39–44. Shell method about other lines Let R be the region bounded by y = x²,x=1, and y=0. Use the shell method to find the volume of the solid generated when R is revolved about the following lines.

y = -2

45–48. Shell and washer methods about other lines Use both the shell method and the washer method to find the volume of the solid that is generated when the region in the first quadrant bounded by y = x²,y=1, and x=0 is revolved about the following lines. 

x = -1

39–44. Shell method about other lines Let R be the region bounded by y = x²,x=1, and y=0. Use the shell method to find the volume of the solid generated when R is revolved about the following lines.

y = 2

Volume of a sphere Let R be the region bounded by the upper half of the circle x²+y² = r² and the x-axis. A sphere of radius r is obtained by revolving R about the x-axis.

a. Use the shell method to verify that the volume of a sphere of radius r is 4/3 πr³.

Volume of a sphere Let R be the region bounded by the upper half of the circle x²+y² = r² and the x-axis. A sphere of radius r is obtained by revolving R about the x-axis.

b. Repeat part (a) using the disk method.

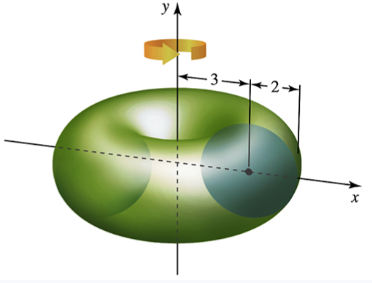
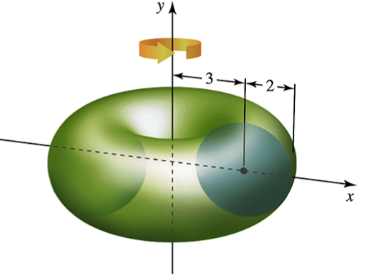
A torus (doughnut) A torus is formed when a circle of radius 2 centered at (3, 0) is revolved about the y-axis.

a. Use the shell method to write an integral for the volume of the torus.

A torus (doughnut) A torus is formed when a circle of radius 2 centered at (3, 0) is revolved about the y-axis.

b. Use the washer method to write an integral for the volume of the torus.

64–68. Shell method Use the shell method to find the volume of the following solids.

A right circular cone of radius 3 and height 8

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

b. If a region is revolved about the y-axis, then the shell method must be used.

64–68. Shell method Use the shell method to find the volume of the following solids.

The solid formed when a hole of radius 3 is drilled symmetrically along the axis of a right circular cone of radius 6 and height 9

53–62. Choose your method Let R be the region bounded by the following curves. Use the method of your choice to find the volume of the solid generated when R is revolved about the given axis.

y = x² and y = 2−x²; about the x-axis

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

a. When using the shell method, the axis of the cylindrical shells is parallel to the axis of revolution.

Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.

c. If a region is revolved about the x-axis, then in principle, it is possible to use the disk/washer method and integrate with respect to x or to use the shell method and integrate with respect to y.

53–62. Choose your method Let R be the region bounded by the following curves. Use the method of your choice to find the volume of the solid generated when R is revolved about the given axis.

y = x−x⁴,y=0; about the x-axis.

53–62. Choose your method Let R be the region bounded by the following curves. Use the method of your choice to find the volume of the solid generated when R is revolved about the given axis.

y = x³,y=0, and x=2; about the x-axis