Back
BackProblem 7.1.35
29–62. Integrals Evaluate the following integrals. Include absolute values only when needed.
∫ₑᵉ^³ dx / (x ln x ln²(ln x))
Problem 7.1.57
29–62. Integrals Evaluate the following integrals. Include absolute values only when needed.
∫₁ᵉ^² (ln x)^5 / x dx
Problem 7.1.67e
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume x > 0 and y > 0.
e. The area under the curve y = 1/x and the x-axis on the interval [1, e] is 1.
Problem 7.1.69
Average value What is the average value of f(x) = 1/x on the interval [1, p] for p > 1? What is the average value of f as p → ∞?
Problem 7.1.74a
ln x is unbounded Use the following argument to show that lim (x → ∞) ln x = ∞ and lim (x → 0⁺) ln x = −∞.
a. Make a sketch of the function f(x) = 1/x on the interval [1, 2]. Explain why the area of the region bounded by y = f(x) and the x-axis on [1, 2] is ln 2.
Problem 7.1.77
Harmonic sum In Chapter 10, we will encounter the harmonic sum 1 + 1/2 + 1/3 + ⋯ + 1/n. Use a left Riemann sum to approximate ∫[1 to n+1] (dx/x) (with unit spacing between the grid points) to show that 1 + 1/2 + 1/3 + ⋯ + 1/n > ln(n + 1). Use this fact to conclude that lim (n → ∞) (1 + 1/2 + 1/3 + ⋯ + 1/n) does not exist.
Problem 7.1.71c
Power lines A power line is attached at the same height to two utility poles that are separated by a distance of 100 ft; the power line follows the curve ƒ(x) = a cosh x/a. Use the following steps to find the value of a that produces a sag of 10 ft midway between the poles. Use a coordinate system that places the poles at x = ±50.
c. Use your answer in part (b) to find a, and then compute the length of the power line.
Problem 7.1.74c
ln x is unbounded Use the following argument to show that lim (x → ∞) ln x = ∞ and lim (x → 0⁺) ln x = −∞.
c. Show that ln 2ⁿ > n/2 and ln 2^(−n) < −n/2.
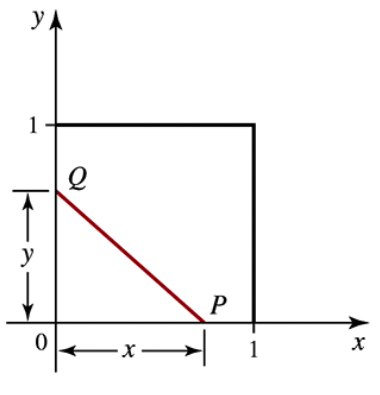
Problem 7.1.78
Probability as an integral Two points P and Q are chosen randomly, one on each of two adjacent sides of a unit square (see figure). What is the probability that the area of the triangle formed by the sides of the square and the line segment PQ is less than one-fourth the area of the square? Begin by showing that x and y must satisfy xy < 1/2 in order for the area condition to be met. Then argue that the required probability is: 1/2 + ∫[1/2 to 1] (dx / 2x) and evaluate the integral.
Problem 7.1.75
Bounds on e Use a left Riemann sum with at least n = 2 subintervals of equal length to approximate ln 2 = ∫[1 to 2] (dt/t) and show that ln 2 < 1. Use a right Riemann sum with n = 7 subintervals of equal length to approximate ln 3 = ∫[1 to 3] (dt/t) and show that ln 3 > 1.
Problem 7.2.7
Suppose a quantity described by the function y(t) = y₀eᵏᵗ, where t is measured in years, has a doubling time of 20 years. Find the rate constant k.
Problem 7.2.54
Geometric means A quantity grows exponentially according to y(t) = y₀eᵏᵗ. What is the relationship among m, n, and p such that y(p) = √(y(m)y(n))?
Problem 7.2.52
"General relative growth rates Define the relative growth rate of the function f over the time interval T to be the relative change in f over an interval of length T:
R_T = [f(t + T) − f(t)] / f(t)
Show that for the exponential function y(t) = y₀ e^{kt}, the relative growth rate R_T, for fixed T, is constant for all t."
Problem 7.2.33
Atmospheric pressure The pressure of Earth’s atmosphere at sea level is approximately 1000 millibars and decreases exponentially with elevation. At an elevation of 30,000 ft (approximately the altitude of Mt. Everest), the pressure is one-third the sea-level pressure. At what elevation is the pressure half the sea-level pressure? At what elevation is it 1% of the sea-level pressure?
Problem 7.2.35
Uranium dating Uranium-238 (U-238) has a half-life of 4.5 billion years. Geologists find a rock containing a mixture of U-238 and lead, and they determine that 85% of the original U-238 remains; the other 15% has decayed into lead. How old is the rock?
Problem 7.2.39
39–40. LED lighting LED (light-emitting diode) bulbs are rapidly decreasing in cost, and they are more energy-efficient than standard incandescent light bulbs and CFL (compact fluorescent light) bulbs. By some estimates, LED bulbs last more than 40 times longer than incandescent bulbs and more than 8 times longer than CFL bulbs. Haitz’s law, which is explored in the following two exercises, predicts that over time, LED bulbs will exponentially increase in efficiency and exponentially decrease in cost.
Haitz’s law predicts that the cost per lumen of an LED bulb decreases by a factor of 10 every 10 years. This means that 10 years from now, the cost of an LED bulb will be 1/10 of its current cost. Predict the cost of a particular LED bulb in 2021 if it costs 4 dollars in 2018.
Problem 7.2.42
Tripling time A quantity increases according to the exponential function y(t) = y₀eᵏᵗ. What is the tripling time for the quantity? What is the time required for the quantity to increase p-fold?
Problem 7.2.44b
A running model A model for the startup of a runner in a short race results in the velocity function v(t) = a(1 - e⁻ᵗ/ᶜ), where a and c are positive constants, t is measured in seconds, and v has units of m/s. (Source: Joe Keller, A Theory of Competitive Running, Physics Today, 26, Sep 1973)
b. Using the velocity in part (a) and assuming s(0) = 0, find the position function s(t), for t ≥ 0.
Problem 7.2.23a
Projection sensitivity
According to the 2014 national population projections published by the U.S. Census Bureau, the U.S. population is projected to be 334.4 million in 2020 with an estimated growth rate of 0.79%/yr.
a. Based on these figures, find the doubling time and the projected population in 2050. Assume the growth rate remains constant.
Problem 7.2.23b
Projection sensitivity
According to the 2014 national population projections published by the U.S. Census Bureau, the U.S. population is projected to be 334.4 million in 2020 with an estimated growth rate of 0.79%/yr.
b. Suppose the actual growth rate is instead 0.7%. What are the resulting doubling time and projected 2050 population?
Problem 7.2.24a
Energy consumption On the first day of the year (t=0), a city uses electricity at a rate of 2000 MW. That rate is projected to increase at a rate of 1.3% per year.
a. Based on these figures, find an exponential growth function for the power (rate of electricity use) for the city.
Problem 7.2.24b
Energy consumption On the first day of the year (t=0), a city uses electricity at a rate of 2000 MW. That rate is projected to increase at a rate of 1.3% per year.
b. Find the total energy (in MW-yr) used by the city over four full years beginning at t=0.
Problem 7.2.24c
Energy consumption On the first day of the year (t=0), a city uses electricity at a rate of 2000 MW. That rate is projected to increase at a rate of 1.3% per year.
c. Find a function that gives the total energy used (in MW-yr) between t=0 and any future time t>0.
Problem 7.2.25
Population of Texas Texas was the third fastest growing state in the United States in 2016. Texas grew from 25.1 million in 2010 to 26.47 million in 2016. Use an exponential growth model to predict the population of Texas in 2025.
Problem 7.2.16
15–20. Designing exponential growth functions Complete the following steps for the given situation.
a. Find the rate constant k and use it to devise an exponential growth function that fits the given data.
b. Answer the accompanying question.
Population The population of Clark County, Nevada, was about 2.115 million in 2015. Assuming an annual growth rate of 1.5%/yr, what will the county population be in 2025?
Problem 7.2.18
15–20. Designing exponential growth functions Complete the following steps for the given situation.
a. Find the rate constant k and use it to devise an exponential growth function that fits the given data.
b. Answer the accompanying question.
Savings account An initial deposit of $1500 is placed in a savings account with an APY of 3.1%. How long will it take until the balance of the account is $2500? Assume the interest rate remains constant and no additional deposits or withdrawals are made.
Problem 7.2.19
15–20. Designing exponential growth functions Complete the following steps for the given situation.
a. Find the rate constant k and use it to devise an exponential growth function that fits the given data.
b. Answer the accompanying question.
Rising costs Between 2010 and 2016, the average rate of inflation was about 1.6%/yr. If a cart of groceries cost $100 in 2010, what will it cost in 2025, assuming the rate of inflation remains constant at 1.6%?
Problem 7.2.20
15–20. Designing exponential growth functions Complete the following steps for the given situation.
a. Find the rate constant k and use it to devise an exponential growth function that fits the given data.
b. Answer the accompanying question.
Cell growth The number of cells in a tumor doubles every 6 weeks starting with 8 cells. After how many weeks does the tumor have 1500 cells?
Problem 7.2.26b
Oil consumption Starting in 2018 (t=0), the rate at which oil is consumed by a small country increases at a rate of 1.5%/yr, starting with an initial rate of 1.2 million barrels/yr.
b. Find the function that gives the amount of oil consumed between t=0 and any future time t.
Problem 7.2.26c
Oil consumption Starting in 2018 (t=0), the rate at which oil is consumed by a small country increases at a rate of 1.5%/yr, starting with an initial rate of 1.2 million barrels/yr.
c. How many years after 2018 will the amount of oil consumed since 2018 reach 10 million barrels?