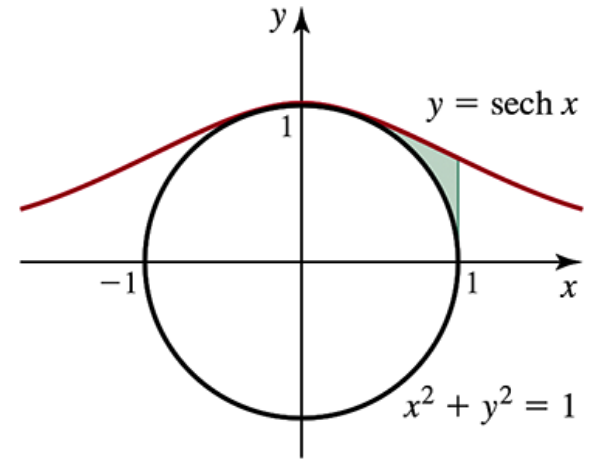
Area of region Find the area of the region bounded by y = sech x, x = 1, and the unit circle (see figure).

Solid of revolution Compute the volume of the solid of revolution that results when the region in Exercise 85 is revolved about the x-axis.

88–91. Limits Use l’Hôpital’s Rule to evaluate the following limits.

lim x → ∞ (1 − coth x) / (1 − tanh x)

88–91. Limits Use l’Hôpital’s Rule to evaluate the following limits.

lim x → 0⁺ (tanh x)ˣ

Newton’s method Use Newton’s method to find all local extreme values of ƒ(x) = x sech x.

Falling body When an object falling from rest encounters air resistance proportional to the square of its velocity, the distance it falls (in meters) after t seconds is given by d(t) = (m/k) ln (cosh (√(kg/m) t)), where m is the mass of the object in kilograms, g = 9.8 m/s² is the acceleration due to gravity, and k is a physical constant.

a. A BASE jumper (m = 75 kg) leaps from a tall cliff and performs a ten-second delay (she free-falls for 10 s and then opens her chute). How far does she fall in 10 s? Assume k = 0.2.

Velocity of falling body Refer to Exercise 95, which gives the position function for a falling body. Use m = 75 kg and k = 0.2.

a. Confirm that the BASE jumper’s velocity t seconds after jumping is v(t) = d'(t) = √(mg/k) tanh (√(kg/m) t).

Velocity of falling body Refer to Exercise 95, which gives the position function for a falling body. Use m = 75 kg and k = 0.2.

c. How long does it take for the BASE jumper to reach a speed of 45 m/s (roughly 100 mi/hr)?

Arc length Use the result of Exercise 108 to find the arc length of the curve: f(x) = ln |tanh(x / 2)| on [ln 2, ln 8].

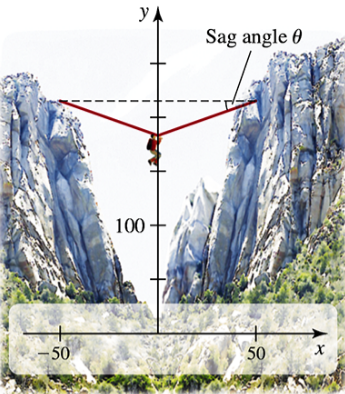
Sag angle Imagine a climber clipping onto the rope described in Example 7 and pulling himself to the rope’s midpoint. Because the rope is supporting the weight of the climber, it no longer takes the shape of the catenary y = 200 cosh x/200. Instead, the rope (nearly) forms two sides of an isosceles triangle. Compute the sag angle θ illustrated in the figure, assuming the rope does not stretch when weighted. Recall from Example 7 that the length of the rope is 101 ft.

Tsunamis A tsunami is an ocean wave often caused by earthquakes on the ocean floor; these waves typically have long wavelengths, ranging from 150 to 1000 km. Imagine a tsunami traveling across the Pacific Ocean, which is the deepest ocean in the world, with an average depth of about 4000 m. Explain why the shallow-water velocity equation (Exercise 75) applies to tsunamis even though the actual depth of the water is large. What does the shallow-water equation say about the speed of a tsunami in the Pacific Ocean (use d = 4000 m)?

Visual approximation

a. Use a graphing utility to sketch the graph of y = coth x and then explain why ∫₅¹⁰ coth x dx ≈ 5.

61–62. Points of intersection and area

a. Sketch the graphs of the functions f and g and find the x-coordinate of the points at which they intersect.

f(x) = sech x, g(x) = tanh x; the region bounded by the graphs of f, g, and the y-axis

61–62. Points of intersection and area

b. Compute the area of the region described.

f(x) = sinh x, g(x) = tanh x; the region bounded by the graphs of f, g, and x = ln 3

63–68. Definite integrals Evaluate the following definite integrals. Use Theorem 7.7 to express your answer in terms of logarithms.

∫₁/₈¹ dx/x√(1 + x²/³)

Inverse identity Show that cosh⁻¹(cosh x) = |x| by using the formula cosh⁻¹ t = ln (t + √(t² – 1)) and considering the cases x ≥ 0 and x < 0.

Terminal velocity Refer to Exercises 95 and 96.

a. Compute a jumper’s terminal velocity, which is defined as lim t → ∞ v(t) = lim t → ∞ √(mg/k) tanh (√(kg/m) t).

Terminal velocity Refer to Exercises 95 and 96.

d. How tall must a cliff be so that the BASE jumper (m = 75 kg and k = 0.2) reaches 95% of terminal velocity? Assume the jumper needs at least 300 m at the end of free fall to deploy the chute and land safely.

Surface area of a catenoid When the catenary y = a cosh x/a is revolved about the x-axis, it sweeps out a surface of revolution called a catenoid. Find the area of the surface generated when y = cosh x on [–ln 2, ln 2] is rotated about the x-axis.

Catenary arch The portion of the curve y =17/15 - cosh x that lies above the x-axis forms a catenary arch. Find the average height of the arch above the x-axis.

A power line is attached at the same height to two utility poles that are separated by a distance of 100 ft; the power line follows the curve ƒ(x) = a cosh x/a. Use the following steps to find the value of a that produces a sag of 10 ft midway between the poles. Use a coordinate system that places the poles at x = ±50.

a. Show that a satisfies the equation cosh 50/a − 1 = 10/a.

Theorem 7.8

Differentiate sinh⁻¹ x = ln (x + √(x² + 1)) to show that d/dx (sinh⁻¹ x) = 1 / √(x² + 1).

101–104. Proving identities Prove the following identities.

cosh (x + y) = cosh x cosh y + sinh x sinh y

Many formulas There are several ways to express the indefinite integral of sech x.

b. Show that ∫ sech x dx = sin⁻¹ (tanh x) + C. (Hint: Show that sech x = sech² x / √(1 − tanh² x) and then make a change of variables.)

"Integral formula Carry out the following steps to derive the formula ∫ csch x dx = ln |tanh(x / 2)| + C (Theorem 7.6).

b. Use the identity for sinh(2u) to show that 2 / sinh(2u) = sech² u / tanh u."

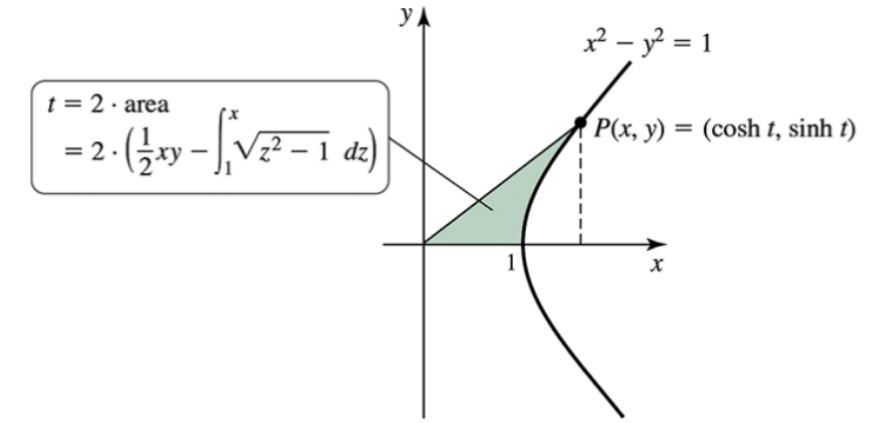
Definitions of hyperbolic sine and cosine Complete the following steps to prove that when the x- and y-coordinates of a point on the hyperbola x² - y² = 1 are defined as cosh t and sinh t, respectively, where t is twice the area of the shaded region in the figure, x and y can be expressed as

x = cosh t = (eᵗ + e⁻ᵗ) / 2 and y = sinh t = (eᵗ - e⁻ᵗ) / 2.

b. In Chapter 8, the formula for the integral in part (a) is derived:

∫ √(z² − 1) dz = (z/2)√(z² − 1) − (1/2) ln|z + √(z² − 1)| + C.

Evaluate this integral on the interval [1, x], explain why the absolute value can be dropped, and combine the result with part (a) to show that:

t = ln(x + √(x² − 1)).

37–56. Integrals Evaluate each integral.

∫ (cosh z) / (sinh² z) dz